如图，二次函数的图像与轴交于点和点，与轴交于点.

(1)求该二次函数的表达式；

(2)过点的直线∥且交抛物线于另一点，求直线的函数表达式；

(3)在(2)的条件下，请解答下列问题：

① 在轴上是否存在一点，使得以、、为顶点的三角形与相似，若存在，求出点的坐标，若不存在，请说明理由；

② 动点以每秒1个单位的速度沿线段从点向点运动，同时，动点 以每秒个单位的速度沿线段从点向点运动，问：在运动过程中，当运动时间为何值时，的面积最大，并求出这个最大值.

如图，在平行四边形中，点、、、分别在边、、、上，，，且平分.

求证：(1)≌；

          (2)四边形是菱形.                

阅读下列材料，并解决相关的问题．

按照一定顺序排列着的一列数称为数列，排在第一位的数称为第1项，记为,依次类推，排在第位的数称为第项，记为.

一般地，如果一个数列从第二项起，每一项与它前一项的比等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母表示（）.如：数列1，3，9，27，…为等比数列，其中，公比为.

则：（1）等比数列3，6，12，…的公比为             ，第4项是                ．

（2）如果一个数列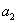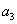，，，，…是等比数列，且公比为，那么根据定义可得到：

，，，…… .

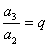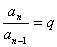所以:，    ，

，

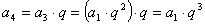由此可得: 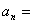                    （用和的代数式表示）.

（3）若一等比数列的公比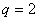，第2项是10，请求它的第1项与第4项.

如图1是“东方之星”救援打捞现场图，小红据此构造出一个如图2所示的数学模型，已知：、、三点在同一水平线上，，，，.

（1）求点到的距离；

（2）求线段的长度.

                     图1                                   图2

小华从家里到学校的路是一段平路和一段下坡路，假设他始终保持平路每分钟走60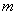，下坡路每分钟走80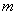,上坡路每分钟走40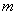，则他从家里到学校需10 ，从学校到家里需15 .问：从小华家到学校的平路和下坡路各有多远？

随着人民生活水平不断提高，我市 “初中生带手机”现象也越来越多，为了了解家

长对此现象的态度，某校数学课外活动小组随机调查了若干名学生家长，并将调查结果进行统计，得出如下所示的条形统计图和扇形统计图.

问：（1）这次调查的学生家长总人数为         .

（2）请补全条形统计图,并求出持“很赞同”态度的学生家长占被调查总人数的百分比.

（3）求扇形统计图中表示学生家长持“无所谓”态度的扇形圆心角的度数.

先化简，再求值：，其中.

如图，在边长均为1的正方形网格纸上有一个

，顶点A、B、C及点O均在格点上，请

按要求完成以下操作或运算：

   （1）将向上平移4个单位，得到  

（不写作法，但要标出字母）；

   （2）将绕点旋转，得到

（不写作法，但要标出字母）；

（3）求点绕着点O旋转到点所经过的路径长.

计算：()+-()+.

如图，在四边形中，，连接，且°,，，则        ．