
科目: 来源: 题型:
如图1,一条抛物线与 轴交于A,B两点(点A在点B的左侧),与
轴交于A,B两点(点A在点B的左侧),与 轴交于点C,且当x=-1和x=3时,
轴交于点C,且当x=-1和x=3时, 的值相等.直线
的值相等.直线 与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
(1)求这条抛物线的表达式.
(2)动点P从原点O出发,在线段OB上以每秒1个单位长度的速度向点B运动,同时动点Q从点B出发,在线段BC上以每秒 2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为
2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为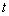 秒.
秒.
①若使△BPQ为直角三角形,请求出所有符合条件的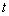 值;
值;
②求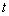 为何值时,四边形ACQ P的面积有最小值,最小值是多少?
为何值时,四边形ACQ P的面积有最小值,最小值是多少?
(3)如图2,当动点P运动到OB的中点时,过点P作PD⊥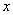 轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿
轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿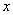 轴向左平移
轴向左平移 个单位长度(
个单位长度( ),将平移后的三角形与△ODM重叠部分的面积记为
),将平移后的三角形与△ODM重叠部分的面积记为 ,求
,求 与
与 的函数关系式.
的函数关系式.
 |
查看答案和解析>>
科目: 来源: 题型:
问题探究】
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45º,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
 |
查看答案和解析>>
科目: 来源: 题型:
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的 倍,且每天包装大黄米和江米的质量之和为45千克.
倍,且每天包装大黄米和江米的质量之和为45千克.
(1)求平均每天包装大黄米和江米的质量各是多 少千克?
少千克?
(2)为迎接今年6月20日的“端午节”,该超市决定在节日前20天增加每天包装大黄米和江米的质量,二者的包装质量与天数的变化情况如图所示,节日后又恢复到原来每天的包装 质量.分别求出在这20天内每天包装大黄米和江米的质量随天数变化的函数关系式,并写出自变量的取值范围.
质量.分别求出在这20天内每天包装大黄米和江米的质量随天数变化的函数关系式,并写出自变量的取值范围.
(3)假设该超市每天都会将当天包装后的大黄米和江米全部出售,已知大黄米成本价为每千克7.9元,江米成本价为每千克9.5元,二者包装费用平均每千克均为0.5元,大黄米售价为每千克10元,江米售价为每千克12元,那么在这20天中有哪几天销售大黄米和江米的利润之和大于120元? [总利润=售价额-成本-包装费用]
 |
查看答案和解析>>
科目: 来源: 题型:
如图,点P是⊙O 外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD= cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
 (3)在(2)的条件下,若点E是
(3)在(2)的条件下,若点E是 的中点,连接CE,求CE的长.
的中点,连接CE,求CE的长.
查看答案和解析>>
科目: 来源: 题型:
如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60 º方向以每小时30海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北1.5海里D处,渔政船航行到点C处时测得点D在南偏东53 º方向上.
(1)求CD两点的距离;
 (2)渔政船决定再次调整航向前去救援,若两船航速不变,并且在点E处相会合,求∠ECD的正弦值. (参考数据:
(2)渔政船决定再次调整航向前去救援,若两船航速不变,并且在点E处相会合,求∠ECD的正弦值. (参考数据: ,
, ,
, )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com