
科目: 来源: 题型:
如图,二次函数y=x2+bx+c的图象交x轴于A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC,动点P以每秒1个单位长度的速度从A向B运动,动点Q以每秒 个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.
个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.
(1)求二次函数的解析 式;
式;
(2)如图1,当△BPQ为直角三角形时,求t的值;
(3)如图2,当t<2时,延长QP交y轴于点M,在抛物线上是否存在 一点N,使得PQ的中点恰为MN的中点?若存在,求出点N的坐标与t的值;若不存在,请说明理由.
一点N,使得PQ的中点恰为MN的中点?若存在,求出点N的坐标与t的值;若不存在,请说明理由.
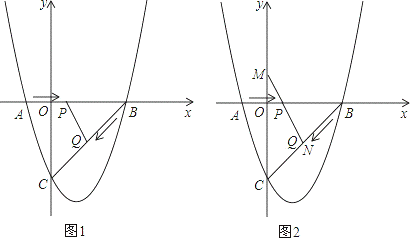
查看答案和解析>>
科目: 来源: 题型:
如图,已知AB是⊙O的直径,过点A作⊙O的切线MA,P为直线MA上一动点,以点P为圆心,PA为半径作⊙P,交⊙O于点C,连接PC、OP、BC.
(1)知识探究(如图1):
①判断直线PC与⊙O的位置关系,请证明你的结论;
②判断直线OP与BC的位置关系,请证明你的结论.
(2)知识运用(如图2):
当PA>OA时,直线PC交AB的延长线于点D,若BD=2AB,求tan∠ABC的值.

查看答案和解析>>
科目: 来源: 题型:
阅读材料:用配方法求最值.
已知x,y为非负实数,
∵x+y﹣2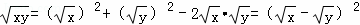 ≥0
≥0
∴x+y≥2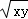 ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立.
示例:当x>0时,求y=x+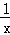 +4的最小值.
+4的最小值.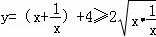 +4=6,当x=
+4=6,当x=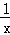 ,即x=1时,y的最小值为6.
,即x=1时,y的最小值为6.
(1)尝试:当x>0时,求y= 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养、维护费用总和为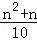 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=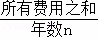 )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
查看答案和解析>>
科目: 来源: 题型:
如图,已知一次函数y=x+b与反比例函数y=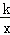 的图象交于A、B两点,其中点A的坐标为(2,3).
的图象交于A、B两点,其中点A的坐标为(2,3).
(1)求一次函数与反比例函数的解析式;
(2)求点B的坐标;
(3)请根据图象直接写出不等式x+b>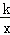 的解集.
的解集.
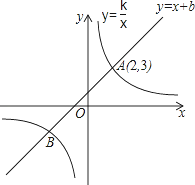
查看答案和解析>>
科目: 来源: 题型:
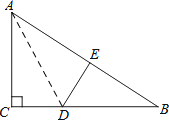
如 图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
( 1)求证:△BDE∽△BAC;
1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目: 来源: 题型:
水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
| 用户月用水量频数分布表 | ||
| 平均用水量(吨) | 频数 | 频率 |
| 3~6吨 | 10 | 0.1 |
| 6~9吨 | m | 0.2 |
| 9~12吨 | 36 | 0.36 |
| 12~15吨 | 25 | n |
| 15~18吨 | 9 | 0.09 |
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= ,n= ;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?

查看答案和解析>>
科目: 来源: 题型:
2015年湘潭市中考招生政策发生较大改变,其中之一是:省级示范性高中批次志愿中,每个考生可填报两所学校(有先后顺序),我市某区域的初三毕业生可填报的省级示范性高中有A、B、C、D四所.
(1)请列举出该区域学生填报省级示范性高中批次志愿的所有可能结果;
(2)求填报方案中含有A学校的概率.
查看答案和解析>>
科目: 来源: 题型:
“东方之星”客船失事之后,本着“关爱生命,救人第一”的宗旨.搜救部门紧急派遣直升机到失事地点进行搜救,搜救过程中,假设直升机飞到A处时,发现前方江面上B处有一漂浮物,从A测得B处的俯角为30°,已知该直升机一直保持在距江面100米高度飞行搜索,飞行速度为10米每秒,求该直升机沿直线方向朝漂浮物飞行多少秒可到达漂浮物的正上方?(结果精确到0.1, ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com