
科目: 来源: 题型:
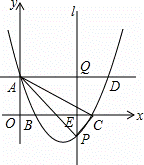
如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>2)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
(1)求抛物线的解析式;
(2)当0<t≤8时,求△AP C面积的最大值;
C面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值; 若不存在,请说明理由.
若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.

查看答案和解析>>
科目: 来源: 题型:
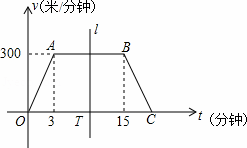
“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.王叔叔某天骑自行车上班从家出发到单位过程中行进速度v(米/分钟)随时间t(分 钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
(1)①当t=2分钟时,速度v= 200 米/分钟,路程s= 200 米;
②当t=15分钟时,速度v= 300 米/分钟,路程s= 4050 米.
(2)当0≤t≤3和3<t≤15时,分别求出路程s(米)关于时间t(分钟)的函数解析式;
(3)求王叔叔该天上班从家出发行进了750米时所用的时间t.
查看答案和解析>>
科目: 来源: 题型:
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.

查看答案和解析>>
科目: 来源: 题型:
某校了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
| 阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题:
(1)分别求出统计表中的x、y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.

查看答案和解析>>
科目: 来源: 题型:
为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元.(注:毛利润=售价﹣进价)
查看答案和解析>>
科目: 来源: 题型:
正比例函数y1=mx(m>0)的图象与反比例函数y2=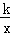 (k≠0)的图象交于点A(n,4)和点B,AM⊥y轴,垂足为M.若△AMB的面积为8,则满足y1>y2的实数x的取值范围是
(k≠0)的图象交于点A(n,4)和点B,AM⊥y轴,垂足为M.若△AMB的面积为8,则满足y1>y2的实数x的取值范围是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com