
科目: 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:填空题
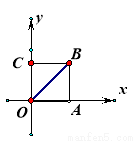
如图,边长为1的正方形ABCO,以A为顶点,且经过点C的抛物线与对角线交于点D,则点D的坐标为 .
查看答案和解析>>
科目: 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1).
①画出“基本图形”关于原点O对称的四边形A1B1C1D1,并填出A1,B1,C1,D1的坐标.
A1( , ) B1( , )
C1( , ) D1( , )
②画出“基本图形”绕B点顺时针旋转900所成的四边形A2B2C2D2 。

查看答案和解析>>
科目: 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
为解方程x4-5x2+4=0,我们可以将x2视为一个整体,然后设x2=y,则 x4=y2,
原方程化为y2-5y+4=0.①
解得y1=1,y2=4
当y=1时,x2=1.∴x=±1
当y=4时,x2=4,∴x=±2。
∴原方程的解为x1=1,x2=-1,x3=2,x4=-2
解答问题:
(1)填空:在由原方程得到方程①的过程中,利用 法达到了降次的目的,体现了 的数学思想.
(2)解方程:(x2-2x)2+x2-2x-6=0.
查看答案和解析>>
科目: 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
已知关于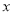 的一元二次方程
的一元二次方程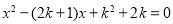 的两个实数根为
的两个实数根为 ,
,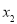 .
.
(1)求k的取值范围。
(2)是否存在实数可k,使得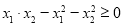 成立?若存在,请求出k值,若不存在,请说明理由.
成立?若存在,请求出k值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值和抛物线与x轴的交点。
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y>0?
查看答案和解析>>
科目: 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,点P是x轴上的一个动点,连结AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.当点P运动到点( ,0)时,求此时DP的长及点D的坐标。
,0)时,求此时DP的长及点D的坐标。

查看答案和解析>>
科目: 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目: 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
如图,抛物线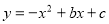 与x轴交与A(1,0),B(- 3,0)两点.
与x轴交与A(1,0),B(- 3,0)两点.
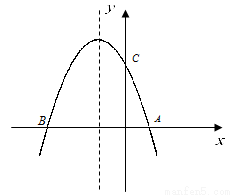
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.
查看答案和解析>>
科目: 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:选择题
已知 是一元二次方程
是一元二次方程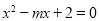 的一个解,则
的一个解,则 的值是( )
的值是( )
A.-3 B.3 C.0 D.0或3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com