
科目: 来源: 题型:
据悉,世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000 00007克,用科学记数法表示此数正确的是( )
00007克,用科学记数法表示此数正确的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
如图,抛物线y=ax2 +bx+c经过点A(-3,0)、C(0,4),点B在抛物线上,CB
∥X轴.且AB平分∠CAO.
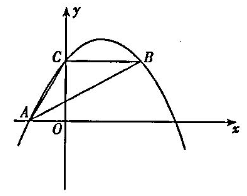
(1)求抛物线的解析式.
(2)线段AB上有一动点P,过P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,直接写出点M的坐标;如果不存在,说明理由,
查看答案和解析>>
科目: 来源: 题型:
)阅读材料:如图1,在△AOB中,∠O=90°,OA=OB,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF=OA.(此结论不必证明,可直接应用)
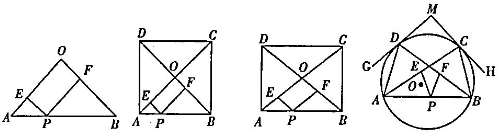 图1 图2 图3 图4
图1 图2 图3 图4
(1)理解与应用
如图2,正方形ABCD的边长为2,对角线AC,BD相交于点O,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则 PE+PF的值为_____________.
(2)类此与推理
如图3,矩形ABCD的对角线AC,BD相交于点O.AB=4,AD=3,点P在AB边上,PE
∥OB交AC于点E,PF∥OA交BD于点F,则PE+PF的值为______________.
(3)拓展与延伸
如图4,⊙○的半径为4,A,B,C,D是⊙○上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD交BD于点F,当∠ADG=∠BCH=30°时,PE+PF是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.
(1)求大桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/时,应控制大桥上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.
查看答案和解析>>
科目: 来源: 题型:
如右图,点A(1,6)和点M(m,n)都在反比例函数y= k (k>0)的图像上.
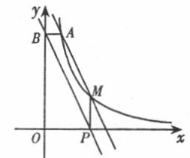
(1)求k的值;
(2)当m=3时,求直线AM的解析式;
(3)当m>1时,过点M作MP上x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
如下图,某翼装飞行员从离水平地面高AC= 500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后柯开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).

查看答案和解析>>
科目: 来源: 题型:
某校计划开设4门选修课:音乐、绘画、体育、舞蹈,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门),对调查结果进行统计后,绘制了如下不完整的两个统计图.
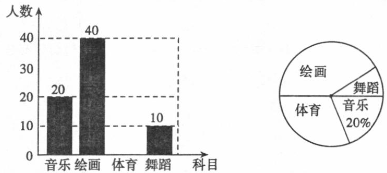
根据以上统计图提供的信息,回答下列问题:
(1)此次调查抽取的学生人数为a=____人,其中选择“绘画”的学生人数占抽样人数的百分比为b=____;
(2)补全条形统计图,并求扇形统计图中“舞蹈”所对应的圆心角的度数;
(3)若该校有2000名学生,请估计全校选择“绘画”的学生大约有多少人?
查看答案和解析>>
科目: 来源: 题型:
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中的点,E、F分别是线段BM、CM的中点.
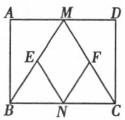
(1)求证:△ABM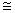 △DCM;
△DCM;
(2)当AB:AD为何值时,四边形MENF是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com