
科目: 来源: 题型:
在△ABC内侧作射线 ,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.
,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.
(1)依题意补全图1;
(2)求证:MD=ME;
(3)如图2,若射线AP平分∠BAC,且AC>AB,求证:MD=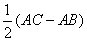 .
.
 | |||
 | |||
查看答案和解析>>
科目: 来源: 题型:
已知:抛物线y=x²+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图像G求图像G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图像有一个公共点,求m的值或取值范围.
查看答案和解析>>
科目: 来源: 题型:
阅读下面材料:小强遇到这样一个问题:
试作一个直角△ABC,使∠C=90°,AB=7,AC+BC=9.
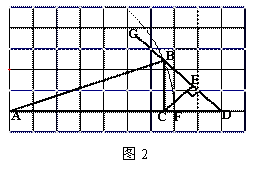
 小强是这样思考的:如图1,假定直角△ABC已作出,延长AC到点D,使CD=CB,则AD=9,∠D=45°,因此可先作出一个辅助△ABD,再作BD的垂直平分线分别交AD于点C,BD于点E,连接BC,所得的△ABC即为所作三角形.具体做法小强是利用图2中1
小强是这样思考的:如图1,假定直角△ABC已作出,延长AC到点D,使CD=CB,则AD=9,∠D=45°,因此可先作出一个辅助△ABD,再作BD的垂直平分线分别交AD于点C,BD于点E,连接BC,所得的△ABC即为所作三角形.具体做法小强是利用图2中1 1正方形网格,通过尺规作图完成
1正方形网格,通过尺规作图完成 的.
的.
(1)请回答:图2中线段AB等于线段 .
(2) 参考小强的方法,解决问题:请在图
参考小强的方法,解决问题:请在图 3的菱形网格中(菱形最小内角为
3的菱形网格中(菱形最小内角为 ,
,
边长为a),画出一个△ABC,使∠C= ,AB=6b,AC+BC=8b.(在图中标明字母,不写作法,保留作图痕迹).
,AB=6b,AC+BC=8b.(在图中标明字母,不写作法,保留作图痕迹).
 | |||
 | |||
‘
查看答案和解析>>
科目: 来源: 题型:
已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于点D,DE⊥CB的延长线于点E.
⑴ 求证:DE为⊙O的切线;
⑵ 若∠A=30°,BE=3,分别求线段DE和  的长.
的长.

查看答案和解析>>
科目: 来源: 题型:
课外阅读是提高学生素养的重要途径.某校为了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间t(小时).根据t的长短分为A,B,C,D四类,下 面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:
面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:
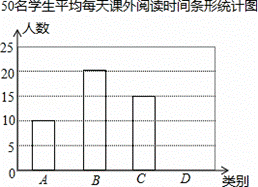 50名学生平均每天课外阅读时间统计表
50名学生平均每天课外阅读时间统计表
| 类别 | 时间t(小时) | 人数 |
| A | t<0.5 | 10 |
| B | 0.5≤t<1 | 20 |
| C | 1≤t<1.5 | 15 |
| D | t≥1.5 | a |
(1)本次调查的样本容量为 ;
(2)求表格中的a的值,并在图中补全条形统计图;
(3)该校现有1200名学生,请你估计该校共有多少名学生课外阅读时间不少于1小时?
查看答案和解析>>
科目: 来源: 题型:
如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.
(1)求证:PB+PC>2AB.
(2)当PC=2,PB= ,∠ACP=45°时,求AB的长.
,∠ACP=45°时,求AB的长.

查看答案和解析>>
科目: 来源: 题型:
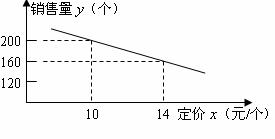
大星发超市进了一批成本为8元/个的文具盒。调查发现:这种文具盒每个星期的 销售量y(个)与它的定价x(元/个)的关系如图所示:
销售量y(个)与它的定价x(元/个)的关系如图所示:
(1)求这种文具盒每个星期的销 售量y(个)与它的定价x(元/个)之间的函数关系式(不必写出自变
售量y(个)与它的定价x(元/个)之间的函数关系式(不必写出自变
量x的取值范围);
(2)每个文具盒定价是多少元时,超市每星期销售这种文具盒(不考虑其他因素)可获得的利润最高?最高利润是多少?
查看答案和解析>>
科目: 来源: 题型:
列方程或方程组解应用题:
周末小明和爸爸准备一起去商场购买一些茶壶和一些茶杯,了解情况后发现甲、乙两家商场都在出售两种同样品牌的茶壶和茶杯,定价相同,茶壶每把定价30元,茶杯每把定价5元,且两家都有优惠.甲商场买一送一大酬宾(买一把茶壶送一只茶杯);乙商场全场九折优惠.小明的爸爸需茶壶5把,茶杯若干只(不少于5只).当去两家商场付款一样时,求需要购买茶杯的数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com