
科目: 来源: 题型:
解:∵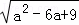 +|b﹣4|=0,
+|b﹣4|=0,
∴ +|b﹣4|=0,
+|b﹣4|=0,
∴|a﹣3|+|b﹣4|=0,
∴a﹣3=0,b﹣4=0,
∴a=3,b=4,
∴直角三角形的斜边长=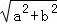 =
=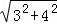 =5.
=5.
查看答案和解析>>
科目: 来源: 题型:
12或7+ . 解:分为两种情况:①斜边是4有一条直角边是3,由勾股定理得:第三边长是
. 解:分为两种情况:①斜边是4有一条直角边是3,由勾股定理得:第三边长是 =
= ,此时周长=3+4+
,此时周长=3+4+ =7+
=7+ ;
;
②3和4都是直角边,由勾股定理得:第三边长是 =5,此时周长=3+4+5=12;
=5,此时周长=3+4+5=12;
综上所述,第三边的长为12或7+ .
.
故答案为:12或7+ .
.

查看答案和解析>>
科目: 来源: 题型:
9.6 解:∵四边形ABCD是平行四边形(已知),
∴OA=OC(平行四边形的对角线相互平分),AB∥CD(平行四边形的对边相互平行),
∴∠DCO=∠BAC(两直线平行,内错角相等);
在△AFO和△CEO中,
 ,
,
则△AFO≌△CEO(ASA),
∴OF=OE,CE=AF(全等三角形的对应边相等);
又∵AD=BC(平行四边形的对边相等),AB=4,AD=3,OF=1.3,
∴四边形BCEF的周长为:BC+EC+OE+OF+BF=AD+AF+2OF+BF=AD+AB+2OF=9.6;
故答案是:9.6.

查看答案和解析>>
科目: 来源: 题型:
5cm≤h≤6cm 解:∵将一根长为18cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,
∴在杯子中筷子最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中筷子最短是等于杯子的高时,x=12,
最长时等于杯子斜边长度是:x= =13,
=13,
∴h的取值范围是:(18﹣13)cm≤h≤(18﹣12)cm,
即5cm≤h≤6cm.
故答案为:5cm≤h≤6cm.
查看答案和解析>>
科目: 来源: 题型:
3 解:∵四边形ABCD是平行四边形,
∴BC=AD=6,
∴S▱ABCD=BC•AE=CD•AF=6×2=12,
∴AF=3.
∴DC边上的高AF的长是3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com