
科目: 来源: 题型:
如图1,△ABC是锐角三角形,过点C作C D⊥AB,垂足为D,
D⊥AB,垂足为D,
则点C到直线AB的距离是 图1
A. 线段CA的长 B.线段CD的长
C. 线段AD的长 D.线段AB的长
 |
查看答案和解析>>
科目: 来源: 题型:
如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.

查看答案和解析>>
科目: 来源: 题型:
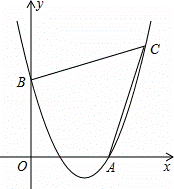
)如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的▱DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边 形AOBC的顶点重合)若能,求出▱DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
形AOBC的顶点重合)若能,求出▱DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是增函数.
例题:证明函数f(x)=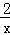 (x>0)是减函数.
(x>0)是减函数.
证明:假设x1<x2,且x1>0,x2>0
f(x1)﹣f(x2)=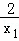 ﹣
﹣ =
=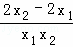 =
=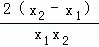
∵x1<x2,且x1>0,x2>0
∴x2﹣x1>0,x1x2>0
∴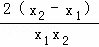 >0,即f(x1)﹣f(x2)>0
>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)=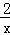 (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
(1)函数f(x)=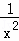 (x>0),f(1)=
(x>0),f(1)=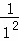 =1,f(2)=
=1,f(2)=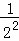 =
=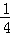 .
.
计算:f(3)= 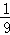 ,f(4)=
,f(4)= 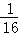 ,猜想f(x)=
,猜想f(x)=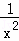 (x>0)是 减 函数(填“增”或“减”);
(x>0)是 减 函数(填“增”或“减”);
查看答案和解析>>
科目: 来源: 题型:
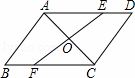
如图,AC是▱ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
(1)求证:△AOE≌△COF;
(2)当EF与AC满足什么条件时,四边形AFCE是菱形?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据: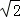 ≈1.41,
≈1.41,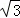 ≈1.73)
≈1.73)
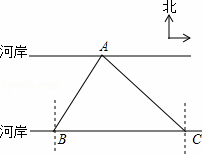
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com