
科目: 来源: 题型:
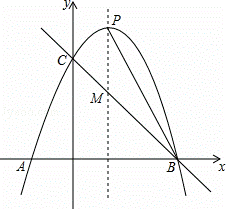
如图,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.
(1)求该抛物线的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△BCD的面积最大?若存在,求出D点坐标及△BCD面积的最大值;若不存 在,请说明理由.
在,请说明理由.
(3)在(1)中的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图1,矩形ABCD的两条边在坐标轴上,点D与坐标原点O重合,且AD=8,AB=6.如图2,矩形ABCD沿OB方向以每秒1个单位长度的速度运动,同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动,当点P到达点C时,矩形ABCD和点P同时停止运动,设点P的运动时间为t秒.

(1)当t=5时,请直接写出点D、点P的坐标;
(2)当点P在线段AB或线段BC上运动时,求出△PBD的面积S关于t的函数关系式,并写出相应t的取值范围;
(3)点P在线段AB或线段BC上运动时,作PE⊥x轴,垂足为点E,当△PEO与△BCD相似时,求出相应的t值.
查看答案和解析>>
科目: 来源: 题型:
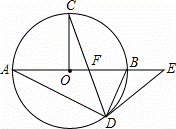
如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求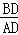 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.
 (1)快艇从港口B到小岛C需要多长时间?
(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.

查看答案和解析>>
科目: 来源: 题型:
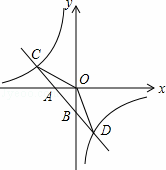
如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=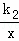 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数y1=k1x+b与反比例函数y2=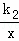 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共80件,且恰好用去1600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价﹣进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
查看答案和解析>>
科目: 来源: 题型:
“热爱劳动,勤俭节约”是中华民族的光荣传统,某小学校为了解本校3至6年级的3000名学生帮助父母做家务的情况,以便做好引导和教育工作,随机抽取了200名学生进行调查,按年级人数和做家务程度,分别绘制了条形统计图(图1)和扇形统计图(图2).
(1)四个年级被调查人数的中位数是多少?
(2)如果把“天天做”、“经常做”、“偶尔做”都统计成帮助父母做家务,那么该校3至6年级学生帮助父母做家务的人数大约是多少?
(3)在这次调查中,六年级共有甲、乙、丙、丁四人“天天帮助父母做家务”,现准备从四人中随机抽取两人进行座谈,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com