
科目: 来源: 题型:
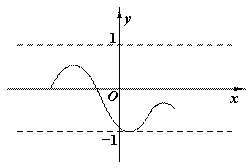
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足﹣M<y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.
(1)分别判断函数y=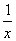 (x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(2)若函数y=﹣x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;
(3)将函数y=x2(﹣1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时,满足 ≤t≤1?
≤t≤1?
查看答案和解析>>
科目: 来源: 题型:
某超市销售多种颜色的服装,其中平均每天销售红、黄、蓝、白4种颜色运动服的数量如下表,由此绘制的不完整的扇形统计图如下图.2-1-c-n-j-y
| 服装颜色 | 红 | 黄 | 蓝 | 白 | 合计 |
| 数量/件 | 20 | n | 40 | 1.5n | m |
| 所对扇形的圆心角 |
| 90° | 360° |

(1)求表中m,n,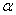 的值,并将扇形统计图补充完整;
的值,并将扇形统计图补充完整;
(2)为吸引更多的顾客,超市将上述扇形统计图制成一个可自由转动的转盘,并规定:顾客在本超市购买商品金额达到一定的数目,就获得一次转动转盘的机会.如果转盘停止后,指针指向红色服装区域、黄色服装区域,可分别获得60元、20元的购物券,求顾客每转动一次转盘获得购物券金额的平均数.
查看答案和解析>>
科目: 来源: 题型:
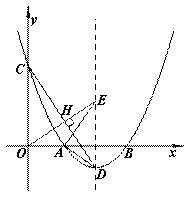
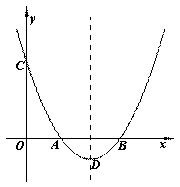
如图,抛物线y=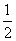 (x-3)2-1与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(x-3)2-1与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(1)试求点A、B、D的坐标;
(2)连接CD,过原点O作OE⊥CD于点H,OE与抛物线的对称轴交于点E,连接AE、AD.求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙O的切线,切点为Q,当PQ的长最小时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
我海军在我国的南海海域举行反潜实战演习.在演习过程中,如图所示,军舰A测得潜艇C的俯角为30°,在军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°.请根据以上数据计算潜艇的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5°,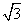 ≈1.7)
≈1.7)

查看答案和解析>>
科目: 来源: 题型:
为了满足铁路交通的快速发展,市政府决定对我市火车站进行改扩建.现有甲、乙两个工程队,甲队单独完成所需时间比乙队单独完成所需时间多5个月,并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍.
(1)求甲、乙两队单独完成这项工程各需几个月?
(2)若甲队每月的施工费为100万元,乙队每月的施工费比甲队多50万元.在保证工程
质量的前提下,为了缩短工期,拟安排甲、乙两队分工合作完成这项工程.在完成这
项工程中,甲队施工时间是乙队施工时间的2倍,那么,甲队最多施工几个月才能使工程款不超过1500万元(甲、乙两队的施工时间按月取整数)?
查看答案和解析>>
科目: 来源: 题型:
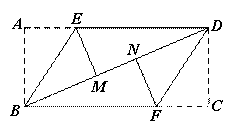
把一张矩形纸片,按如下图所示操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.
查看答案和解析>>
科目: 来源: 题型:
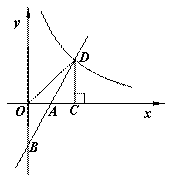
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=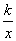 (x>0)交于D点,过点D作DC⊥x轴于点C,连接OD.已知△AOB≌△ACD. www-2-1-cnjy-com
(x>0)交于D点,过点D作DC⊥x轴于点C,连接OD.已知△AOB≌△ACD. www-2-1-cnjy-com
(1)若b=﹣2,求双曲线的解析式;
(2)试探究k与b的数量关系,并写出直线OD的解析式.
查看答案和解析>>
科目: 来源: 题型:
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+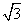 .其中正确的序号是_________________(把你认为正确的都填上).
.其中正确的序号是_________________(把你认为正确的都填上).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com