
科目: 来源: 题型:
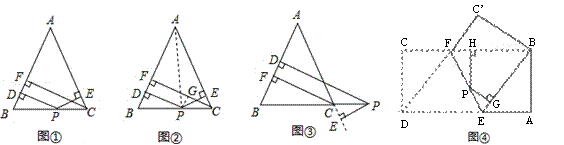
【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥ AB,垂足为F.求证:PD+PE=CF.小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF. 小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
AB,垂足为F.求证:PD+PE=CF.小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF. 小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
(1) 从小军 和小俊的思路中任选一种方法,证明PD+PE=CF。
和小俊的思路中任选一种方法,证明PD+PE=CF。
【变式探究】
(2) 如图3,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;
【结论 运用】请运用上述解答中所积累的经验和方法完成下列题目:
运用】请运用上述解答中所积累的经验和方法完成下列题目:
(3) 如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=16,CF=6,求PG+PH的值;
查看答案和解析>>
科目: 来源: 题型:
如图,由两个等宽的矩形叠合而得到四边形ABCD.
(1) 试判断四边形ABCD的形状并证明。
(2) 若矩形长为8cm,宽为2cm,求四边形ABCD的最大面积。
若矩形长为8cm,宽为2cm,求四边形ABCD的最大面积。
 |
查看答案和解析>>
科目: 来源: 题型:
如图,正方形ABCD的顶点C在直线a上,
且BM 直线a于M,DN
直线a于M,DN 直线a于N
直线a于N
(1) 求证:MN=BM+DN
(2) 若点B,D到a的距离分别是1,2.求正方形ABCD的面积。
 |
查看答案和解析>>
科目: 来源: 题型:
在三只乒乓球上,分别写有三个不同的正整数(用a、b、c表示),三只乒乓球除上面的数字不同外,其余均相同.将三只乒乓球放在一个盒子中,无放回的从中依次摸2只乒乓球,将球上面的数字相加求和.当和为偶数时,记为事件A;当和为奇数时,记为事件B.
(1) 设计一组a、b、c的值,使得事件A为必然发生的事件;
(2) 设计一组a、b、c的值,使得事件B发生的概率大于事件A发生的概率.
查看答案和解析>>
科目: 来源: 题型:
我校八年级共有1300名学生,准备调查他们对“低碳”知识的了解程度.
(1) 在确定调查方式时,团委设计了以下三种方案:
方案一:调查八年级部分女生;
方案二:调查八年级部分男生;
方案三:到八年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是______________;
(2) 团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;

(3) 请你估计我校八年级约有多少名学生比较了解“低碳”知识。
查看答案和解析>>
科目: 来源: 题型:
如图,在直角坐标系中,A(0,4),B(-3,0).
(1) ①画出线段AB关于y轴对称线段AC;
②将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD ;
;
(2) 判断四边形ABCD的形状:____。
(3) 若直线y=kx平分(1)中四边形ABCD的面积,请直接写出 实数k的值.
实数k的值.

查看答案和解析>>
科目: 来源: 题型:
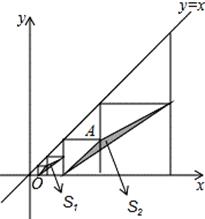
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右 第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则S10的值为 .
第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则S10的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com