
科目: 来源: 题型:
如果有两点到一条直线的距离相等,那么称这条直线为 “两点的等距线”.
(1)如图1,直线CD经过线段AB的中点P,试说明直线CD是点A、B的一条等距线.
(2)如图2,A、B、C是正方形网格中的三个格点,请在网格中作出所有的直线m,使直线m过点C且直线m是“A、B的等距线”.


 (3)如图3,抛物线
(3)如图3,抛物线 过点
过点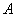 (,
(, ),
), (3,
(3, ),顶点为C.抛物线上是否存在点P ,使
),顶点为C.抛物线上是否存在点P ,使 ,若存在,求出点P的坐标;若不存在,请说明理由。
,若存在,求出点P的坐标;若不存在,请说明理由。
| |||
| |||
查看答案和解析>>
科目: 来源: 题型:
宁波某水果店计划购进甲、乙两种新出产的水果共140千克,
| 进价(元/千克) | 售价(元/千克) | |
| 甲种 | 5 | 8 |
| 乙种 | 9 | 13 |
这两种水果的进价、售价如表所示:
(1)若该水果店预计进货款为1000元,则这两种水果各购进多少千克?
(2)若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,应怎样安排进货才能使水果点在销售完这批水果时获利最多?此时利润为多少元?
查看答案和解析>>
科目: 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线,交BC于点E.
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,
试判断△ABC的形状,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
实施新课程改革后,学生的自主学习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调査,并将调査结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调査结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题 :
:
(1)本次调查中,张老师一共调査了 名同学,其中C类女生有 名,
D类男生有 名。
(2)将上面的条形统计图补充完整。
(3)为了共同进步,张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法 求出所选两位同学恰好是一位男同学和一位女同学的概率。
求出所选两位同学恰好是一位男同学和一位女同学的概率。

查看答案和解析>>
科目: 来源: 题型:
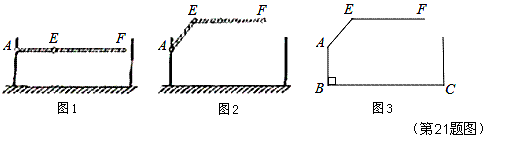
某地下车库出口处“两段式栏杆”如图1所示,点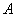 是栏杆转动的支点,点
是栏杆转动的支点,点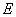 是栏杆两段的连接点.当车辆经过时,栏杆
是栏杆两段的连接点.当车辆经过时,栏杆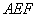 升起后的位置如图2所示,其示意图如图3所示,其中
升起后的位置如图2所示,其示意图如图3所示,其中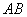 ⊥
⊥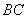 ,
, 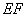 ∥
∥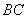 ,
,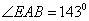 ,
,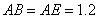 米,求当车辆经过时,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离).(结果精确到0.1米,栏杆宽度忽略不计参考数据:sin 37° ≈ 0
米,求当车辆经过时,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离).(结果精确到0.1米,栏杆宽度忽略不计参考数据:sin 37° ≈ 0 .60,cos 37° ≈ 0.80,tan 37° ≈ 0.75.)
.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75.)
查看答案和解析>>
科目: 来源: 题型:
如图,在矩形ABCD中,AB=3,AD=4,将此矩形折叠,使点D落在AB边上的点E处,折痕为FH,点C落在点Q处,EQ与BC交于 点G,设AE=x,四边形EFHQ的面积为y,则y关于x的函数解析式是 .
点G,设AE=x,四边形EFHQ的面积为y,则y关于x的函数解析式是 .

查看答案和解析>>
科目: 来源: 题型:
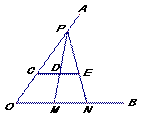
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,点C为线段OP上任意一点, CD∥ON交PM、PN分别为D、E, 若MN=3,则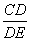 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com