已知一个布袋里装有2个红球，3个白球和a个黄球，这些球除颜色外其余都相同．若从该布袋里任意摸出1个球，是红球的概率为，则a等于（　　）

A、1           B、2            C、3            D、4

如图，AB是⊙O的直径，点D,C在⊙O上，AD//OC, ∠DAB=60⁰,连接AC,则∠DAC等于（    ）

A、20°        B、30°        C、25°           D、40°

两圆的圆心都是O，半径分别为r₁，r₂（r₁<r₂）,若r₁<OP< r₂，则点P在（     ）

A、大圆外        B、小圆内       C、大圆内，小圆外        D、无法确定

下列事件中，是必然事件的是（     ）

A、任意抛掷一枚硬币，出现正面

B、从2、4、6、8、10这5张卡片中任抽一张是奇数

C、从装有一个红球三个黄球的袋子中任取两球，至少有一个是黄球

D、投掷一枚普通骰子，朝上一面的点数是3

抛物线的顶点坐标为（    ）

A、（3，-1）      B、（-3,  1）      C、（-3，-1）     D、（3,  1）

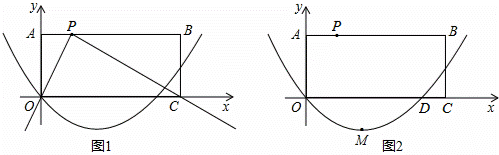
在平面直角坐标系xOy中，矩形ABCO的顶点A、C分别在y轴、x轴正半轴上，点P在AB上，PA=1，AO=2．经过原点的抛物线y=mx²-x+n的对称轴是直线x=2．
（1）求出该抛物线的解析式．
（2）如图1，将一块两直角边足够长的三角板的直角顶点放在P点处，两直角边恰好分别经过点O和C．现在利用图2进行如下探究：
①将三角板从图1中的位置开始，绕点P顺时针旋转，两直角边分别交OA、OC于点E、F，当点E和点A重合时停止旋转．请你观察、猜想，在这个过程中，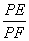

的值是否发生变化？若发生变化，说明理由；若不发生变化，求出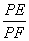的值．
②设（1）中的抛物线与x轴的另一个交点为D，顶点为M，在①的旋转过程中，是否存在点F，使△DMF为等腰三角形？若不存在，请说明理由．

某市政府大力扶持大学生创业，李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=-10x+500．
（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？
（成本=进价×销售量）

如图，在⊙O中，AB，CD是两条直径，M为OB上一点，CM的延长线交⊙O于点E，连结DE．

(1)　求证：；

(2)　若M为OB的中点，AB=8，DE=时，求MC的长．

（1）如图，EF是⊙O的直径，请用尺规作⊙O的内接正方形ABCD，要求所作正方形的一组对边AD、BC垂直于EF. (见示意图；不写作法，保留作图痕迹)；

（2）连结EA、EB，求出∠EAD、∠EBC的度数.

  如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE,点F落在AD上.

（1）求证：△ABF∽△DFE

（2）若△BEF也与△ABF相似，请求出的值 .