
科目: 来源: 题型:
D.
【解析】根据题意得:∠BAE=∠ADC=∠AFE=90°,∴∠AEF+∠EAF=90°,∠DAC+∠ACD=90°,∴∠AEF=∠ACD,∴①中两三角形相似; 容易判断△AFE∽△BAE,得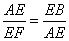 ,
,
又∵AE=ED,∴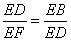 而∠BED=∠BED,∴△FED∽△DEB.故②正确;
而∠BED=∠BED,∴△FED∽△DEB.故②正确;
∵AB∥CD,∴∠BAC=∠GCD,∵∠ABE=∠DAF,∠EBD=∠EDF,且∠ABG=∠ABE+∠EBD,
∴∠ABG=∠DAF+∠EDF=∠DFC;∵∠ABG=∠DFC,∠BAG=∠DCF,∴△CFD∽△ABG,故③正确;所以相似的有①②③.
故选D.
查看答案和解析>>
科目: 来源: 题型:
如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连结BE交AC于F,连结FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD②△FED与△DEB③△CFD与△ABG④△ADF与△CFB中相似的为( )

A.①④ B.①② C.②③④ D.①②③
查看答案和解析>>
科目: 来源: 题型:
C.
【解析】如果将图①看作是铺成的一个1×1的正方形图案,图②看作是铺成的一个2×2的正方形图案,图③看作是铺成的一个3×3的正方形图案,图④看作是铺成的一个4×4的正方形图案,那么根据给出的四个图形的规律可以知道,组成大正方形的每个小正方形上有一个完整的圆,因此圆的数目是大正方形边长的平方;又每四个小正方形组成一个完整的圆,这样的圆的个数是大正方形的边长减1的平方,从而可得第10个图中完整的圆共有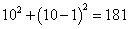 个.
个.
故选C.
查看答案和解析>>
科目: 来源: 题型:
如图①是一块瓷砖的图案,用这种瓷砖铺设地面,如果铺设成如图②的图案,其中完整的圆一共有5个,如果铺设成如图③的图案,其中完整的圆一共有13个,如果铺设成如图④的图案,其中完整的圆一共有25个,以此规律下去,第10个图中,完整的圆一共有( ).
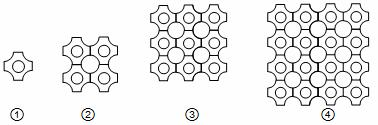
A.100个 B.101个 C.181个 D.221个
查看答案和解析>>
科目: 来源: 题型:
B.
【解析】连接BE,由AB是直径得∠AEB=90°,由CD⊥AB得∠ACF=90°,进一步可以证得△ACF∽△AEB,所以 ,所以AE×AF=AC×AB,即AE×AF=12.
,所以AE×AF=AC×AB,即AE×AF=12.
故选B.

查看答案和解析>>
科目: 来源: 题型:
如图,AB是⊙O的直径且AB=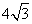 ,点C是OA的中点,过点C[,作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE·AF的值为( ).
,点C是OA的中点,过点C[,作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE·AF的值为( ).
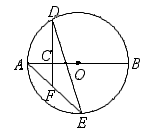
A .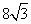 B.
B. C.
C. D.
D.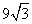
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com