
科目: 来源: 题型:
如图1,小明将量角器和一块含30 °角的直角三角板ABC紧靠着放在同一平面内,使直角边BC与量角器的0°线CD在同一直线上(即点B、C、O、D在同一直线上),O为量角器圆弧所在圆的圆心,∠ACB=90°,∠CAB=30°, BC=6cm.
°角的直角三角板ABC紧靠着放在同一平面内,使直角边BC与量角器的0°线CD在同一直线上(即点B、C、O、D在同一直线上),O为量角器圆弧所在圆的圆心,∠ACB=90°,∠CAB=30°, BC=6cm.
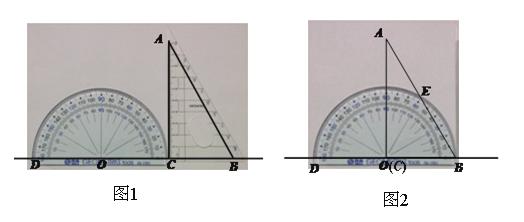
(1)判断AC是不是⊙O的切线,并说明理由.
(2)将直角三角板ABC沿CD方向平移,使点C落在点O上.此时点B落在点C原位置上(如图2),AB交⊙O于点E,则弧BE的长是多少?
查看答案和解析>>
科目: 来源: 题型:
定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
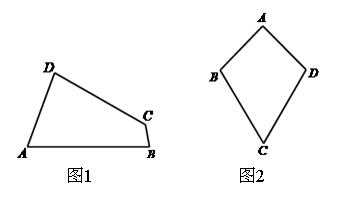
(1)已知:如图1,四边形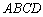 是“等对角四边形”,
是“等对角四边形”,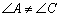 ,
,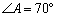 ,
, .求
.求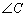 ,
,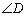 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形”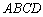 (如图2),其中
(如图2),其中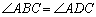 ,
,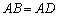 ,此时她发现
,此时她发现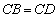 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形”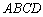 中,
中, ,
,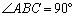 ,
,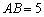 ,
,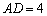 .求对角线
.求对角线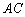 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
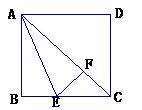
(1)观察图形,写出图中与BE相等的线段.
(2)选择图中与BE相等的任意一条线段,并加以证明.
查看答案和解析>>
科目: 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线,交BC于点E.
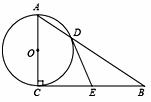
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至 C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向。

(1)求海警船距离事故船C的距离BC.
(2)若海警船以40海里/小时的速度前往救援,求海警船到达事故船C处大约所需的时间.(温馨提示:sin 53°≈0.8,cos 53°≈0.6)
查看答案和解析>>
科目: 来源: 题型:
草莓是我地区的特色时令水果,草莓一上市,水果店的老板用1200元购进一批草莓很快售完;老板又用2500元购进第二批草莓,所购箱数是第一批的2倍,但进价比第一批每箱多了5元.
(1)第一批草莓每箱进价多少元?
(2)老板以每箱150元的价格销售第二批草莓,售出80%后,为了尽快售完,决定打折促销,要使第二批草莓的销售利润不少于320元,剩余的草莓每箱售价至少打几折? (利润=售价﹣进价)
查看答案和解析>>
科目: 来源: 题型:
实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期三个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
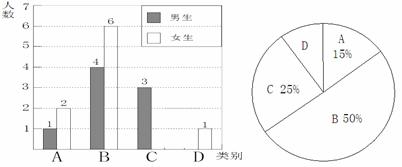
(1)本次调查中,张老师一共调查了 名同学,其中C类女生有 名, D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com