
科目: 来源: 题型:
阅读材料:如图1,在平面直角坐标系中,A.B两点的坐标分别为A(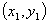 ,B
,B ,AB中点P的坐标为
,AB中点P的坐标为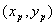 .由
.由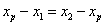 ,得
,得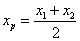 ,同理
,同理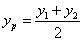 ,所以AB的中点坐标为(
,所以AB的中点坐标为(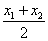 ,
, ).由勾股定理得
).由勾股定理得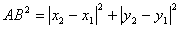 ,所以A、B两点间的距离公式为AB=
,所以A、B两点间的距离公式为AB=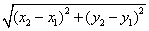 .
.
注:上述公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
如图2,直线l: 与抛物线
与抛物线 交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.


(1)求A、B两点的坐标及P、C两点的坐标;
(2)连结AB、AC,求证:△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
查看答案和解析>>
科目: 来源: 题型:
如图,正方形ABCD和正方形AEFG有公共的顶点A,连BG、DE,M为DE的中点,连AM.
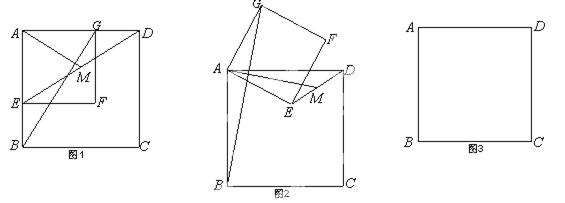
(1)如图1,AE、AG分别与AB、AD重合时,AM和BG的大小和位置关系分别是 、_ ____;
(2)将图1中的正方形AEFG绕A点旋转到如图2,则(1)中的结论是否仍成立?试证明你的结论;
(3)若将图1中的正方形AEFG绕A点逆时针旋转到正方形ABCD外时,则AM和BG的大小和位置关系分别是__________、____________,请你在图3中画出图形,并直 接写出结论,不要求证明.
接写出结论,不要求证明.
查看答案和解析>>
科目: 来源: 题型:


 操作:小英准备制作一个表面积为6cm2的正方体纸盒,现选用一些废弃的纸片进行如下设计:
操作:小英准备制作一个表面积为6cm2的正方体纸盒,现选用一些废弃的纸片进行如下设计:
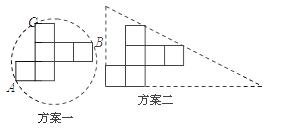
说明:
方案一:图形中的圆过点A.B.C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点.
纸片利用率= ×100%
×100%
发现:(1)小英发现方案一中的点A.B恰好为该圆一直径的两个端点.你认为小英的这个发现是否正确,请说明理由.
(2)小英通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.(结果精确到0.1%)
探究:(3)小英感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.(结果精确到0.1%)
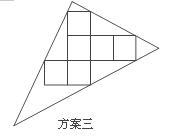
说明:方案三中的每条边均过其中两个正方形的顶点.
查看答案和解析>>
科目: 来源: 题型:
已知直线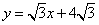 与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于C.
与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于C.
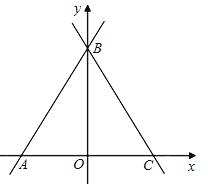
(1)求直线BC的解析式;
(2)若动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿C-B-A向点A运动(不与C、A重合),动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围;
(3)在(2)的条件下,当t=4秒时,y轴上有一点M,平 面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图,设∠BAC=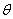 (0°<
(0°<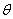 <90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A
<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A 开始,用等长的小棒依次向右摆放,其中 A
开始,用等长的小棒依次向右摆放,其中 A A
A 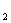 为第一根小棒,且 A
为第一根小棒,且 A A
A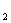 =AA
=AA

(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)若已经摆放了3根小棒,则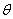 1 = ,
1 = ,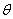 2= ,
2= , 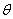 3= ;(用含
3= ;(用含 的式子表示)
的式子表示)
(3)若只能摆放4根小棒,求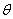 的范围.
的范围.
查看答案和解析>>
科目: 来源: 题型:
如图,已知反比例函数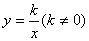 的图象经过点(
的图象经过点(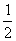 ,8),直线
,8),直线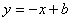 经过该反比例函数图象上的点Q(4,
经过该反比例函数图象上的点Q(4, ).
).

(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与 轴、
轴、 轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
查看答案和解析>>
科目: 来源: 题型:
如图,现有边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC 于H,折痕为EF,联结BP、BH.
于H,折痕为EF,联结BP、BH.
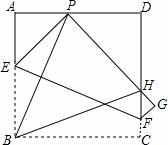
(1)求证:∠APB=∠BPH;
(2)求证:AP+ HC=PH;
HC=PH;
(3)当AP=1时,求PH的长.
查看答案和解析>>
科目: 来源: 题型:
某五金店购进 一批数量足够多的p型节能电灯 进价为35元/只,以50元/只销售,每天销售20只.市场调研发现:若每只每降l元,则每天销售数量比原来多3只.现商店决定对Q型节能电灯进行降价促销活动,每只降价x元(x为正整数).在促销期间,商店要想每天获得最大销售利润,每只应降价多少元?每天最大销售毛利润为多少?(注:每只节能灯的销售毛利润指每只节能灯的销售价与进货价的差)
一批数量足够多的p型节能电灯 进价为35元/只,以50元/只销售,每天销售20只.市场调研发现:若每只每降l元,则每天销售数量比原来多3只.现商店决定对Q型节能电灯进行降价促销活动,每只降价x元(x为正整数).在促销期间,商店要想每天获得最大销售利润,每只应降价多少元?每天最大销售毛利润为多少?(注:每只节能灯的销售毛利润指每只节能灯的销售价与进货价的差)
查看答案和解析>>
科目: 来源: 题型:
某公交公司的公共汽车和出租车每天从沂源出发往返于沂源和济南两地,出租车比公共汽车多往返一趟,如图表示出租车距沂源的路程 (单位:千米)与所用时间
(单位:千米)与所用时间 (单位:小时)的函数图象.已知公共汽车比出租车晚1小时出发,到达济南后休息2小时,然后按原路原速返回,结果比出租车最后一次返回沂源早1小时.
(单位:小时)的函数图象.已知公共汽车比出租车晚1小时出发,到达济南后休息2小时,然后按原路原速返回,结果比出租车最后一次返回沂源早1小时.
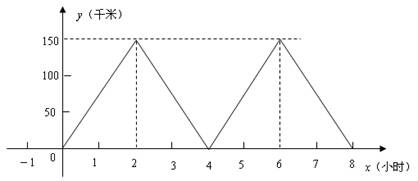
(1)请在图中画出公共汽车距沂源的路程 (千米)与所用时间
(千米)与所用时间 (小时)的函数图象;
(小时)的函数图象;
(2)求两车在途中相遇的次数(直接写出答案);
(3)求两车最后一次相遇时,距沂源的路程.
查看答案和解析>>
科目: 来源: 题型:
从﹣1,1,2这三个数字中,随机抽取一个数,记为a,那么,使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形的面积为 ,且使关于x的不等式组
,且使关于x的不等式组 有解的概率为 .
有解的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com