
科目: 来源: 题型:
如图,一大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx+c,小王骑自行车从O匀速沿直线到拱梁一端A,再匀速通过拱梁部分的桥面AC,小王从O到A用了2秒, 当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面AC共需
当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面AC共需  秒.
秒.


查看答案和解析>>
科目: 来源: 题型:
如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m) 与运行的水平距离x(m)满足关系式
与运行的水平距离x(m)满足关系式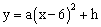 。已知球网与O点
。已知球网与O点 的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围);
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求 二次函数中二次项系数a的最大值。
二次函数中二次项系数a的最大值。

查看答案和解析>>
科目: 来源: 题型:
在青岛市开展的创城活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园
 ,花园的一边靠墙,另三边用总长为40m的栅栏围
,花园的一边靠墙,另三边用总长为40m的栅栏围 成(如图所示).若设花园的
成(如图所示).若设花园的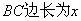
 (m),花园的面积为
(m),花园的面积为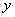

 (m
(m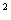
 ).
).
(1)求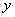
 与
与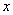
 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量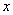
 的取值范围;
的取值范围;
(2)满足条件的花园面积能达到200 m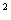
 吗?若能,求出此时
吗?若能,求出此时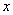
 的值;若不能,说明理由;
的值;若不能,说明理由;
(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当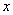
 取何值时,花园的面积最大?最大面积为多少?
取何值时,花园的面积最大?最大面积为多少?

查看答案和解析>>
科目: 来源: 题型:
市政府为改善居民的居住环境,修建了环境幽雅的环城公园,为了给公园内的草评定期喷水,安装了一些自动旋转喷水器,如图所示,设喷水管
 高出地面1.5m,在
高出地面1.5m,在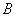
 处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头
处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头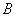
 与水流最高点
与水流最高点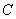
 的连线与地平面成
的连线与地平面成
 的角,水流的最高点
的角,水流的最高点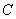
 离地平面距离比喷水头
离地平面距离比喷水头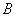
 离地平面距离高出2m,水流的落地点为
离地平面距离高出2m,水流的落地点为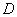
 .在建立如图所示的直角坐标系中:
.在建立如图所示的直角坐标系中:
(1)求抛物线的函数解析式;
(2)求水流的落地点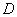
 到
到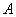
 点的距离是多少m?
点的距离是多少m?
查看答案和解析>>
科目: 来源: 题型:
已知 抛
抛 物线y=ax2﹣2x+c与y轴交于x轴上方,与x轴没有交点,那么该抛物线的顶点所在的象限是【 】
物线y=ax2﹣2x+c与y轴交于x轴上方,与x轴没有交点,那么该抛物线的顶点所在的象限是【 】
A.第四象限 B.第三象限 C.第二象限 D.第一象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com