
科目: 来源: 题型:
探究与发现:
探究一:我们知道,三角形的一个外角等 于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图,∠FDC与 ∠ECD
∠ECD 分别为△ADC的两个外角,
分别为△ADC的两个外角,
试探究∠A与∠FDC+∠ECD的数量关系.
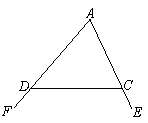

探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
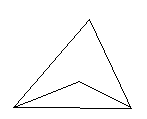

探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠AD C和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
C和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.


探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠ A+∠B+∠E+∠F的数量关系: _______________________________.
A+∠B+∠E+∠F的数量关系: _______________________________.

查看答案和解析>>
科目: 来源: 题型:
已知点A(0,0),B(0,3),C(4,t+3),D(4,t). 记N(t)为□ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为【 】
A.6、7 B.7 、8 C.6、7、8 D.6、8、9
、8 C.6、7、8 D.6、8、9
查看答案和解析>>
科目: 来源: 题型:
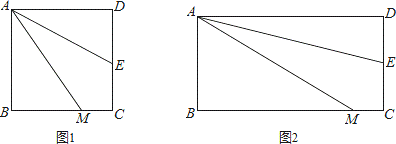
【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请 说明理由.
说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

查看答案和解析>>
科目: 来源: 题型:
操作发现
将一副直角三角板如图①摆放,能够发现等腰直角三角板A BC的斜边与含30°角的直角三角板DEF的长直
BC的斜边与含30°角的直角三角板DEF的长直 角边DE重合.
角边DE重合.
问题解决
 将图①中的等腰直角三角板ABC绕点B
将图①中的等腰直角三角板ABC绕点B 顺时针旋转30°,点C落在BF上,AC与
顺时针旋转30°,点C落在BF上,AC与 BD交于点O,连接CD,如图②.
BD交于点O,连接CD,如图②.
(1)求证:AD∥BF;
(2)若AD=2,求AB的长.
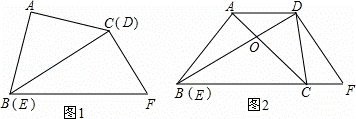
查看答案和解析>>
科目: 来源: 题型:
已知矩形纸片ABCD中,AB=1,BC=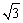 ,将该纸片叠成一个平面图形,折痕EF不经过A点(E、F是该矩形边界上的点),折叠后点A落在A′处,给出以下判断:
,将该纸片叠成一个平面图形,折痕EF不经过A点(E、F是该矩形边界上的点),折叠后点A落在A′处,给出以下判断:
①当四边形A,CDF为矩形时,EF=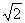 ;
;
②当EF=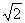 时,四边形A′CDF为矩形;
时,四边形A′CDF为矩形;
③当EF=2时,四边形BA′CD为等腰梯形;
④当四边形BA′CD 为等腰梯形时,EF=2。
为等腰梯形时,EF=2。

其中正确的是  (把所有正确结论序号都填在横线上)。
(把所有正确结论序号都填在横线上)。
查看答案和解析>>
科目: 来源: 题型:
如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在点A′、D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD 时,
时,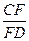 的值为( )
的值为( )

A.
B.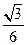 C.
C.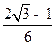
D.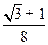
查看答案和解析>>
科目: 来源: 题型:
如图1,将由5个边长为1的小正方形组成的十字形纸板沿虚线剪拼成一个大正方形,需剪4
刀。
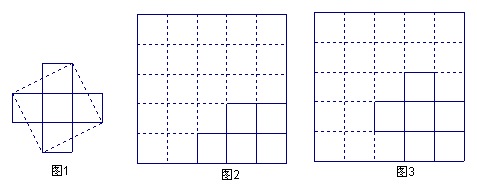

思考发现:大正方形的面积等于5个小正方形的面积和,大正方形的边长等于_______。
实践操作:如图2,将网格中5个边长为1的小正方形组成的图形纸板剪拼成一个大正方形,要求剪
两刀,画出剪拼的痕迹。
智力开发:将网格中的5个边长为1的正方形组成的十字形纸 板,要求只剪2刀也拼成一个大正方形。
板,要求只剪2刀也拼成一个大正方形。
在图中用虚线画出剪拼的痕迹。
查看答案和解析>>
科目: 来源: 题型:
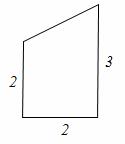
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角 梯形,其中三边长分别为2、2、3,则原直角三角形纸片
梯形,其中三边长分别为2、2、3,则原直角三角形纸片 的斜边长是 。
的斜边长是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com