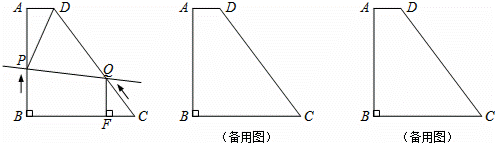
如图，已知直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，AB=8，CD=10．

（1）求梯形ABCD的面积；

（2）动点P从点B出发，以2个单位/s的速度沿B→A→D→C方向向点C运动；动点Q从点C出发，以2个单位/s的速度沿C→D→A方向向点A运动；过点Q作QF⊥BC于点F．若P、Q两点同时出发，当其中一点到达终点时另一点也随之停止运动，设运动时间为t秒．问：

①当点P在B→A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值，并判断此时PQ是否平分梯形ABCD的面积；若不存在，请说明理由．

②在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

阅读材料：

例：说明代数式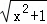+ 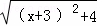的几何意义，并求它的最小值．

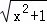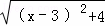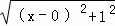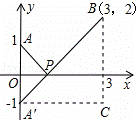
解：+=+，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则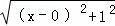可以看成点P与点A（0，1）的距离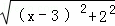，可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA+PB的最小值．

设点A关于x轴的对称点为A′，则PA=PA′，因此，求PA+PB的最小值，只需求PA′+PB的最小值，而点A′、B间的直线段距离最短，所以PA′+PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C=3，CB=3，所以A′B=3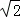，即原式的最小值为3．

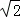根据以上阅读材料，解答下列问题：

（1）代数式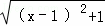+的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B（2，3）或（2，﹣3）的距离之和．（填写点B的坐标）

（2）代数式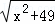+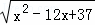的最小值．

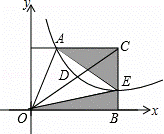
如图，在平面直角坐标系xOy中，梯形AOBC的边OB在x轴的正半轴上，AC∥OB，BC⊥OB，过点A的双曲线y=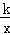的一支在第一象限交梯形对角线OC于点D，交边BC于点E．

（1）填空：双曲线的另一支在第三象限，k的取值范围是k＞0；

（2）若点C的坐标为（1，1），请用含有k的式子表示阴影部分的面积S．并回答：当点E在什么位置时，阴影部分面积S最小？

（3）若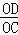=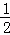，S_△OAC=2，求双曲线的解析式．

如图，在Rt△ABC中，∠C=90°，点P为AC边上的一点，将线段AP绕点A顺时针方向旋转（点P对应点P′），当AP旋转至AP′⊥AB时，点B、P、P′恰好在同一直线上，此时作P′E⊥AC于点E．

（1）求证：∠CBP=∠ABP；

（2）求证：AE=CP；

（3）当，BP′=5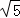时，求线段AB的长．

已知关于x的方程x²﹣2（k﹣1）x+k²=0有两个实数根x₁，x₂．

（1）求k的取值范围；

（2）若|x₁+x₂|=x₁x₂﹣1，求k的值．

雅安地震牵动着全国人民的心，某单位开展了“一方有难，八方支援”赈灾捐款活动．第一天收到捐款10 000元，第三天收到捐款12 100元．

（1）如果第二天、第三天收到捐款的增长率相同，求捐款增长率；

（2）按照（1）中收到捐款的增长率速度，第四天该单位能收到多少捐款？

钓鱼岛自古以来就是我国的神圣领土，为维护国家主权和海洋权利，我国海监和渔政部门对钓鱼岛 海域实现了常态化巡航管理．如图，某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B，B船在A船的正东方向，且两船保持20海里的距离，某一时刻两海监船同时测得在A的东北方向，B的北偏东15°方向有一我国渔政执法船C，求此时船C与船B的距离是多少．（结果保留根号）

先化简，再求值：（﹣）÷，其中，a是方程x²+3x+1=0的根．

（3x+1）²=4（x﹣2）²．

x²﹣5x+6=0