
科目: 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:解答题
某省为解决农村饮用水问题,省财政部门共投资10亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2012年,A 市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2014年该市计划投资“改水工程”864万元.
(1)求A市投资“改水工程”的年平均增长率;
(2)从2012年到2014年,A市三年共投资“改水工程”多少万元?
查看答案和解析>>
科目: 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:解答题
如图,矩形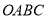 的顶点
的顶点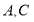 分别在
分别在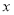 轴和
轴和 轴上,点
轴上,点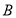 的坐标为
的坐标为 .双曲线
.双曲线 的图像经过
的图像经过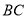 的中点
的中点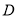 ,且与
,且与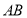 交于点
交于点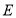 ,连接
,连接 .
.
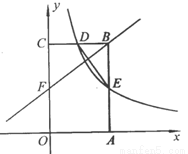
(1)求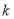 的值及点
的值及点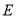 的坐标;
的坐标;
(2)若点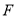 是边上一点,且ΔFCB∽ΔDBE,求直线
是边上一点,且ΔFCB∽ΔDBE,求直线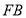 的解析式
的解析式
查看答案和解析>>
科目: 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:解答题
如图所示,在⊙O中,  ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
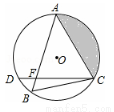
(1)求证:AC2=AB•AF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.
查看答案和解析>>
科目: 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:解答题
今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的两种统计图表.

对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)请补全图中所示数的条形统计图;
(3)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”等级中的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,记下数字后放回袋中,另一人再从袋中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
查看答案和解析>>
科目: 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:解答题
如图,在RtΔABC中,∠BAC=90°,DB⊥BC,DA=DB,点E是BC的中点,DE与AB相交于点G.

(1)求证DE⊥AB;
(2)如果∠FCB==∠FBC=∠DAB,设DF与BC交于点H,求证:DH=FH.
查看答案和解析>>
科目: 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:解答题
某市自来水公司为了鼓励市民节约用水,于2014年4月开始采用以用户为单位按月分段收费办法收取水费,新按月分段收费标准如下:
标准一:每月用水不超过20吨(包括20吨)的水量,每吨收费2.45元
标准二:每月用水超过20吨但不超过30吨的水量,按每吨 元收费;
元收费;
标准三:超过30吨的部分,按每吨( +1.62)元收费。(说明:a>2.45).
+1.62)元收费。(说明:a>2.45).
(1)居民甲4月份用水25吨,交水费65.4元,求a的值;
(2)若居民甲2014年4月以后,每月用水x(吨),应交水费y(元),求y与x之间的函数关系式,并注明自变量x的取值范围;
(3)随着夏天的到来,各家的用水量在不但增加.为了节省开支,居民甲计划自家6月份的水费不能超过家庭月收入的2%(居民甲家的月收入为6540元),则居民甲家六月份最多能用水多少吨?
查看答案和解析>>
科目: 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:解答题
如图,在正方形ABCD中, AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
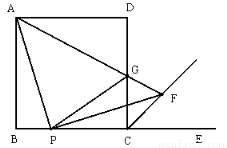
(1)求证:∠GCF=∠FCE;
(2)判断线段PG,PB与DG之间的数量关系,并证明你的结论;
(3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形,若存在,求出BM的长度,若不存在,说明理由.
查看答案和解析>>
科目: 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,已知OA=2,OC=4,⊙M与 轴相切于点C,与
轴相切于点C,与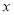 轴交于A,B两点,∠ACD=90°,抛物线
轴交于A,B两点,∠ACD=90°,抛物线 经过A,B,C三点.
经过A,B,C三点.

(1)求证:∠CAO=∠CAD;
(2)求弦BD的长;
(3)在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com