
科目: 来源:2014-2015学年北京市延庆县中考一模数学试卷(解析版) 题型:解答题
如图,一次函数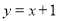 的图象与反比例函数
的图象与反比例函数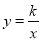 (
(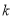 为常数,且
为常数,且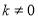 )的图象都经过点A(m,2).
)的图象都经过点A(m,2).

(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数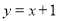 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
查看答案和解析>>
科目: 来源:2014-2015学年北京市延庆县中考一模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题:八年级的学生去距学校10千米的科技馆参观,一部分学生骑自行车先走,过了20分钟,其余的学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑自行车学生速度的2倍,求骑车学生每小时走多少千米?
查看答案和解析>>
科目: 来源:2014-2015学年北京市延庆县中考一模数学试卷(解析版) 题型:解答题
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长.
查看答案和解析>>
科目: 来源:2014-2015学年北京市延庆县中考一模数学试卷(解析版) 题型:解答题
某区对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:
A.使用清洁能源 B.汽车限行
C.绿化造林 D.拆除燃煤小锅炉
调查过程随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:(1)这次被调查的市民共有 人.
(2)请你将统计图1补充完整.
(3)已知该区人口为200000人,请根据调查结果估计该市认同汽车限行的人数.

查看答案和解析>>
科目: 来源:2014-2015学年北京市延庆县中考一模数学试卷(解析版) 题型:解答题
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.

(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使CD = BC,连接AD与CM交于点E,若⊙O的半径为2,ED =1,求AC的长.
查看答案和解析>>
科目: 来源:2014-2015学年北京市延庆县中考一模数学试卷(解析版) 题型:解答题
数学活动﹣求重叠部分的面积
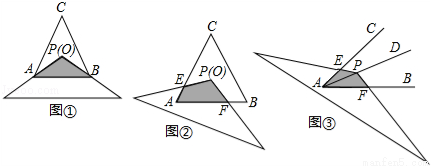
(1)问题情境:如图①,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点P与等边△ABC的内心O重合,已知OA=2,则图中重叠部分△PAB的面积为  .
.
(2)探究1:在(1)的条件下,将纸片绕P点旋转至如图②所示位置,纸片两边分别与AC,AB交于点E,F,图②中重叠部分的面积与图①重叠部分的面积是否相等?如果相等,请给予证明;如果不相等,请说明理由.
(3)探究2:如图③,若∠CAB=α(0°<α<90°),AD为∠CAB的角平分线,点P在射线AD上,且AP=2,以P为顶点的等腰三角形纸片(纸片足够大)与∠CAB的两边AC,AB分别交于点E、F,∠EPF=180°﹣α,求重叠部分的面积.(用α或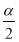 的三角函数值表示)
的三角函数值表示)
查看答案和解析>>
科目: 来源:2014-2015学年北京市延庆县中考一模数学试卷(解析版) 题型:解答题
二次函数 的图象经过点A(﹣1,4),B(1,0),
的图象经过点A(﹣1,4),B(1,0), 经过点B,且与二次函数
经过点B,且与二次函数 交于点D.过点D作DC⊥x轴,垂足为点C.
交于点D.过点D作DC⊥x轴,垂足为点C.
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在BD上方),过N作NP⊥x轴,垂足为点P,交BD于点M,求MN的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com