
科目: 来源: 题型:
在一个不透明的盒子中装有12个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是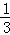 ,则黄球的个数为( )
,则黄球的个数为( )
A. 18 B. 20 C. 24 D. 28
查看答案和解析>>
科目: 来源: 题型:
一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )

A. 预 B. 祝 C. 成 D. 功
查看答案和解析>>
科目: 来源: 题型:
贵阳数博会于2015年5月26日至29日在贵阳国际会议展览中心举行,贵阳副市长刘春成介绍在近两年签约投资额已经超过了1.4×103多亿元.1.4×103这个数可以表示为( )
A. 14 B. 140 C. 1400 D. 14000
查看答案和解析>>
科目: 来源: 题型:
已知矩形ABCD中,AB=10cm,AD=4cm,作如下折叠操作.如图1和图2所示,在边AB上取点M,在边AD或边DC上取点P.连接MP.将△AMP或四边形AMPD沿着直线MP折叠得到△A′MP或四边形A′MPD′,点A的落点为点A′,点D的落点为点D′.
探究:
(1)如图1,若AM=8cm,点P在AD上,点A′落在DC上,则∠MA′C的度数为 ;
(2)如图2,若AM=5cm,点P在DC上,点A′落在DC上,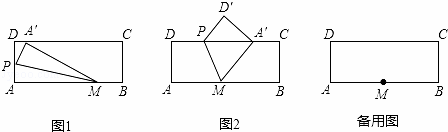
①求证:△MA′P是等腰三角形;
②直接写出线段DP的长.
(3)若点M固定为AB中点,点P由A开始,沿A﹣D﹣C方向.在AD,DC边上运动.设点P的运动速度为1cm/s,运动时间为ts,按操作要求折叠.
①求:当MA′与线段DC有交点时,t的取值范围;
②直接写出当点A′到边AB的距离最大时,t的值;
发现:
若点M在线段AB上移动,点P仍为线段AD或DC上的任意点.随着点M位置的不同.按操作要求折叠后.点A的落点A′的位置会出现以下三种不同的情况:
不会落在线段DC上,只有一次落在线段DC上,会有两次落在线段DC上.
请直接写出点A′由两次落在线段DC上时,AM的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
如图,足球上守门员在O处开出一高球.球从离地面1米的A处飞出(A在y轴上),把球看成点.其运行的高度y(单位:m)与运行的水平距离x(单位:m)满足关系式y=a(x﹣6)2+h.
(1)①当此球开出后.飞行的最高点距离地面4米时.求y与x满足的关系式.
②在①的情况下,足球落地点C距守门员多少米?(取4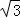 ≈7)
≈7)
③如图所示,若在①的情况下,求落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.求:站在距O带你6米的B处的球员甲要抢到第二个落点D处的求.他应再向前跑多少米?(取2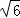 =5)
=5)
(2)球员乙升高为1.75米.在距O点11米的H处.试图原地跃起用头拦截.守门员调整开球高度.若保证足球下落至H正上方时低于球员乙的身高.同时落地点在距O点15米之内.求h的取值范围.
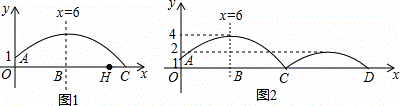
查看答案和解析>>
科目: 来源: 题型:
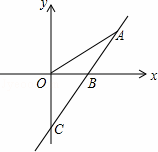
如图,直线y=kx﹣4与x轴,y轴分别交于B、C两点.且∠OBC=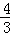 .
.
(1)求点B的坐标及k的值;
(2)若点A时第一象限内直线y=kx﹣4上一动点.则当△AOB的面积为6时,求点A的坐标;
(3)在(2)成立的条件下.在坐标轴上找一点P,使得∠APC=90°,直接写出P点坐标.
查看答案和解析>>
科目: 来源: 题型:
中国是世界上13个贫水国家之一.某校有800名在校学生,学校为鼓励学生节约用水,展开“珍惜水资源,节约每一滴水”系列教育活动.为响应学校号召,数学小组做了如下调查:
小亮为了解一个拧不紧的水龙头的滴水情况,记录了滴水时间和烧杯中的水面高度,
如图1.小明设计了调查问卷,在学校随机抽取一部分学生进行了问卷调查,并制作出统计图.如图2和图3.
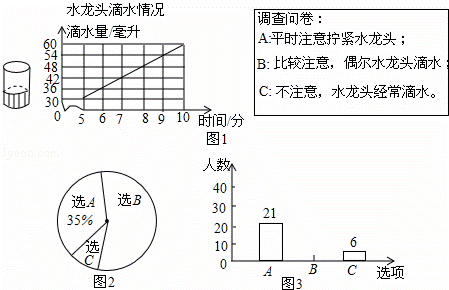
经结合图2和图3回答下列问题:
(1)参加问卷调查的学生人数为 人,其中选C的人数占调查人数的百分比为 .
(2)在这所学校中选“比较注意,偶尔水龙头滴水”的大概有 人.若在该校随机抽取一名学生,这名学生选B的概率为 .
请结合图1解答下列问题
(3)在“水龙头滴水情况”图中,水龙头滴水量(毫升)与时间(分)可以用我们学过的哪种函数表示?请求出函数关系式.
(4)为了维持生命,每人每天需要约2400毫升水,该校选C的学生因没有拧紧水龙头,2小时浪费的水可维持多少人一天的生命需要?
查看答案和解析>>
科目: 来源: 题型:
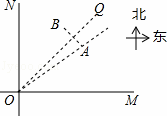
如图,某城市中心的两条公路OM和ON,其中OM为东西走向,ON为南北走向,A、B是两条公路所围区域内的两个标志性建筑.已知A、B关于∠MON的平分线OQ对称.OA=1000米,测得建筑物A在公路交叉口O的北偏东53.5°方向上.
求:建筑物B到公路ON的距离.
(参考数据:sin53.5°=0.8,cos53.5°=0.6,tan53.5°≈1.35)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com