
科目: 来源: 题型:
已知,△ABC 是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
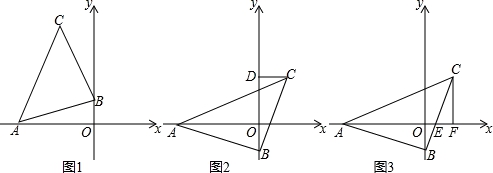
(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,﹣1),求点C的坐标;
(2)如图2,过点C作CD⊥y轴于D,请直接写出线段OA、OD、CD之间等量关系;
(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于F,问CF与AE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
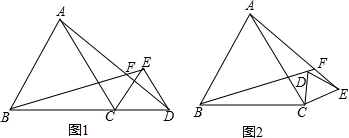
(1)如图1,C为线段BD上的一个动点(不与点B、D重合),在BD同侧分别作等边△ABC和等边△CDE,AD与BE相交于点F,求证:△ACD≌△BCE.
(2)将△CDE绕C点旋转至如图2,在旋转过程中,∠AFB的大小是否发生改变?若不改变,请求出∠AFB的度数;若改变,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
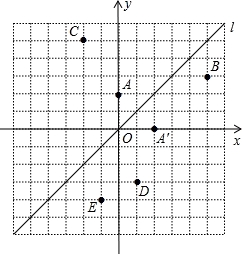
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′__________、C′__________;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为__________(不必证明);
运用与拓广:
(3)已知两点D(1,﹣3)、E(﹣1,﹣4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
查看答案和解析>>
科目: 来源: 题型:
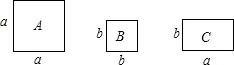
如图,正方形卡片A类、B类和长方形卡片C类各有若干张,如果要拼一个长为(a+2b),宽为(a+b)的大长方形,求需要A、B、C类卡片各多少张?并请用这些卡片拼出符合条件的长方形(画出示意图,并标明卡片类型即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com