
科目: 来源: 题型:
在平面直角坐标系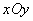 中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点
中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点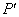 为射线CP上一点,满足
为射线CP上一点,满足
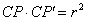 ,则称点
,则称点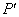 为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点
为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点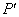 的示意图.
的示意图.
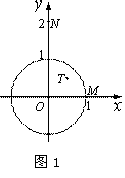
(1) 如图1,当⊙O的半径为1时,分别求出点M(1,0),N(0,2),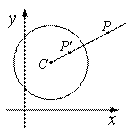
T(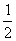 ,
,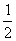 )关于⊙O的反演点
)关于⊙O的反演点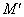 ,
,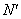 ,
,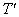 的坐标;
的坐标;
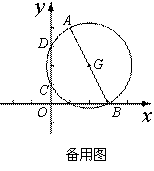
(2) 如图2,已知点A(1,4),B(3,0),以AB为直径的⊙G与y轴交于点C,D(点C位于点D下方),E为CD的中点.
① 若点O,E关于⊙G的反演点分别为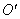 ,
,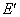 ,求∠
,求∠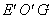 的大小;
的大小;
 ② 若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为
② 若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为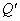 ,请直接写出线段
,请直接写出线段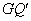 的长度.
的长度.
 | |||
 | |||
查看答案和解析>>
科目: 来源: 题型:
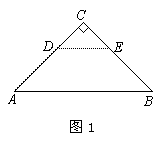
如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度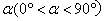 ,使点A,D,E在同一直线上,连接AD,BE.
,使点A,D,E在同一直线上,连接AD,BE.
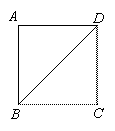
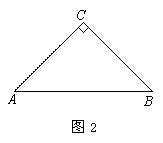
(1) ① 依题意补全图2;
② 求证:AD=BE,且AD⊥BE;
③ 作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
 (2) 如图3,正方形ABCD边长为
(2) 如图3,正方形ABCD边长为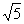 ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
 |  | ||||
| |||||
查看答案和解析>>
科目: 来源: 题型:
在平面直角坐标系 中,抛物线
中,抛物线 经过点A(
经过点A( ,t),B(3,t),与y轴交于点C(0,
,t),B(3,t),与y轴交于点C(0, ).一次函数
).一次函数 的图象经过抛物线的顶点D.
的图象经过抛物线的顶点D.
(1) 求抛物线的表达式;
(2) 求一次函数 的表达式;
的表达式;
(3) 将直线 :
: 绕其与y轴的交点E旋转,使当
绕其与y轴的交点E旋转,使当 时,直线
时,直线 总位于抛物线的下方,请结合函数图象,求
总位于抛物线的下方,请结合函数图象,求 的取值范围.
的取值范围.

查看答案和解析>>
科目: 来源: 题型:
有这样一个问题:探究函数 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1) 函数 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2) 下表是y与x的几组对应值.
| x | … |
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | 5 | … |
| y | … |
|
|
|
|
|
|
|
| 3 |
| m |
| … |
求m的值;
(3) 如下图,在平面直角坐标系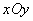 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(4) 进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):
.
查看答案和解析>>
科目: 来源: 题型:
如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
 (2)若AB=2,sin∠D=
(2)若AB=2,sin∠D= ,求AE的长.
,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据: ≈1.41,
≈1.41,
 ≈1.73,
≈1.73, ≈2.45,)
≈2.45,)
 |
查看答案和解析>>
科目: 来源: 题型:
如图,一次函数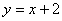 的图象与反比例函数
的图象与反比例函数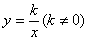 的图象交于A,B两点,且点A的坐标为(1,m).
的图象交于A,B两点,且点A的坐标为(1,m).
(1) 求反比例函数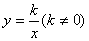 的表达式;
的表达式;
(2) 若P是y轴上一点,且满足△ABP的面积为6,求点P的坐标.
 |
查看答案和解析>>
科目: 来源: 题型:
已知二次函数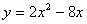 .
.
(1) 用配方法将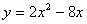 化成
化成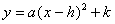 的形式;
的形式;
(2) 求出该二次函数的图象与x轴的交点A,B的坐标(A在B的左侧);
(3) 将该二次函数的图象沿x轴向左平移2个单位,再沿y轴向上平移3个单位,请直接写出得到的新图象的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
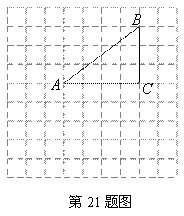
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
(1) 在网格中画出△AB1C1;
(2) 计算点B旋转到B1的过程中所经过的路径长.(结果保留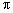 )
)
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com