
科目: 来源: 题型:
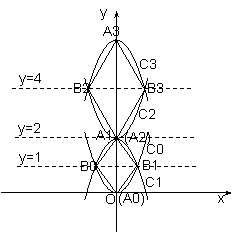
如图,已知抛物线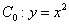 ,顶点记作
,顶点记作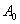 .首先我们将抛物线
.首先我们将抛物线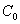 关于直线
关于直线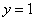 对称翻折过去得到抛物线
对称翻折过去得到抛物线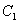 称为第一次操作,再将抛物线
称为第一次操作,再将抛物线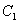 关于直线
关于直线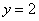 对称翻折过去得到抛物线
对称翻折过去得到抛物线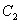 称为第二次操作,…,将抛物线
称为第二次操作,…,将抛物线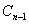 关于直线
关于直线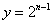 对称翻折过去得到抛物线
对称翻折过去得到抛物线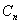 (顶点记作
(顶点记作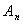 )称为第n此操作(n=1,2,3…),….设抛物线
)称为第n此操作(n=1,2,3…),….设抛物线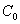 与抛物线
与抛物线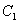 交于两点
交于两点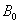 与
与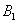 ,顺次连接
,顺次连接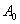 、
、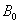 、
、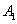 、
、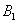 四个点得到四边形
四个点得到四边形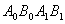 ,抛物线
,抛物线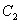 与抛物线
与抛物线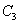 交于两点
交于两点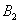 与
与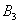 ,顺次连接
,顺次连接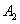 、
、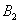 、
、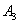 、
、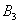 四个点得到四边形
四个点得到四边形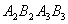 ,…,抛物线
,…,抛物线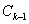 与抛物线
与抛物线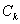 交于两点
交于两点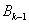 与
与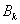 ,顺次连接
,顺次连接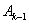 、
、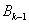 、
、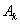 、
、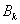 四个点得到四边形
四个点得到四边形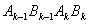 (k=1,3,5…),….
(k=1,3,5…),….
(1)请分别直接写出抛物线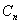 (n=1,2,3,4)的解析式;
(n=1,2,3,4)的解析式;
 (2)一系列四边形
(2)一系列四边形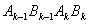 (k=1,3,5…)
(k=1,3,5…)
为哪种特殊的四边形(说明理由)?它们
都相似吗?如果全都相似,请证明之;如
果不全都相似,请举出一对不相似的反例;
(3)试归纳出抛物线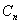 的解析式,无需证明.
的解析式,无需证明.
并利用你归纳出来的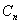 的解析式
的解析式
求四边形 (k=1,3,5…)
(k=1,3,5…)
的面积(用含k的式子表示).
查看答案和解析>>
科目: 来源: 题型:
已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE;∠DAB=∠CAE,连接DC与BE,G、F分别是DC与BE的中点.
(1)探索发现:
如图1,若∠DAB=60°,则∠AFG= ; 如图2,若∠DAB=90°,则∠AFG= ;
(2)探究证明:如图3,若∠DAB=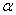 ,试探究∠AFG与
,试探究∠AFG与 的数量关系?并给予证明;
的数量关系?并给予证明;
(3)动手实践:
如果∠ACB为锐角,AB≠AC,∠BAC≠90°,点M在线段BC上运动,连接AM,以AM为一边,以点A为直角顶点,且在AM的右侧作等腰直角△AMN,连接NC;试探究:若NC⊥BC(点C、M重合除外),则∠ACB等于多少度?请同学们自己动手画出相应图形,并说明理由.(画图不写作法)
查看答案和解析>>
科目: 来源: 题型:
已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,
点A的对应点C恰好落在⊙O上.
(1)当P在AB上方而C在AB下方时(如图1),判断PO与BC的位置关系,并证明你的判断;
(2)当P、C都在AB上方时(如图2),过C点作CD⊥直线AP于D,且PC=2PD,证明:CD是⊙O的切线.
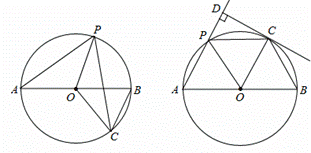
图1 图2
查看答案和解析>>
科目: 来源: 题型:
智能手机如果安装了一款测量软件“Smart Measure”后,就可以测量物高、宽度和面积等.如图,打开软件后将手机摄像头的屏幕准星对准脚部按键,再对准头部按键,即可测量出人体的高度.其数学原理如图②所示,测量者AB与被测量者CD都垂直于地面BC.
(1)若手机显示AC=1m,AD=1.8m,∠CAD=60°,求此时CD
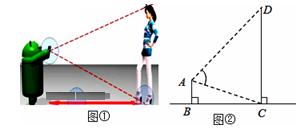
的高.(结果保留根号)
(2)对于一般情况,试探索手机设定的测量高度的公式:设AC=a,AD=b,∠CAD=α,即用a、b、α来表示CD.(提示: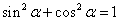 )
)
查看答案和解析>>
科目: 来源: 题型:
为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).根据上述信息,解答下列各题:
(1)该班级女生人数是 ,女生收看“两会
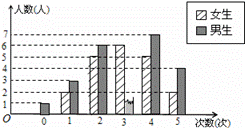
”新闻次数的中位数是 ;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
| 统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
| 该班级男生 | 3 | 3 | 4 | 2 | … |
比较该班级男、女生收看“两会”新闻次数的波动大小.
查看答案和解析>>
科目: 来源: 题型:
某市一公交线路共设置六个站点,分别为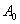 ,
,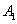 ,
,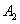 ,
,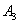 ,
,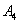 ,
,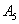 .现有甲乙两人同时从
.现有甲乙两人同时从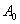 站点上车,且他们中的每个人在站点
站点上车,且他们中的每个人在站点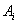 (i=1,2,3,4,5)下车是等可能的.
(i=1,2,3,4,5)下车是等可能的.
(1)求甲在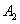 站点下车的概率;
站点下车的概率;
(2)求甲,乙两人不在同一站点下车的概率.
四、(本大题共4小题,每小题各8分,共32分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com