
科目: 来源: 题型:
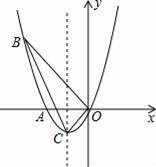
如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,且以AO为边的四边形AODE是平行四边形,求点D的坐标.
(3)P是抛物线上第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
(1)问题发现
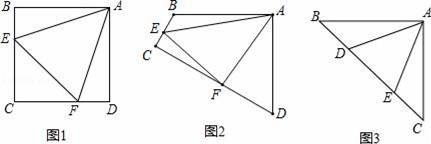
如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程.

查看答案和解析>>
科目: 来源: 题型:
在圣诞节前夕,几位同学到某文具店调查一种进价为2元的圣诞贺卡的销售情况,每张定价3元,每天能卖出500张,每张售价每上涨0.1元,其每天销售量就减少10个.另外,物价局规定,售价不得超过商品进价的240%.据此,请你解答下面问题:
(1)要实现每天800元的利润,应如何定价?
(2)800元的利润是否最大?如何定价,才能获得最大利润?
查看答案和解析>>
科目: 来源: 题型:
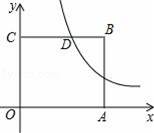
如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数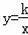
 (x>0,k≠0)的图象经过线段BC的中点D.
(x>0,k≠0)的图象经过线段BC的中点D.
(1)求k的值;
(2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.

查看答案和解析>>
科目: 来源: 题型:
一架空客A320﹣200型客机2014年12月28日从印尼泗水飞往新加坡途中失事.我国政府马上派出舰船搜救,我海军一艘潜艇在海面下500米A点处测得仰角为30°正前方的海底有疑似黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有疑似黑匣子信号发出,求海底疑似黑匣子C点处距离海面的深度?(结果保留根号)


查看答案和解析>>
科目: 来源: 题型:
某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
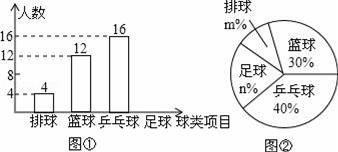

(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目: 来源: 题型:
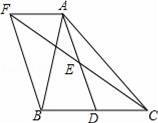
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
(3)在(2)的条件下,△ABC满足条件 ,矩形AFBD是正方形.

查看答案和解析>>
科目: 来源: 题型:
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2,点E在x轴上,若△ACE为直角三角形,则E的坐标是 .
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2,点E在x轴上,若△ACE为直角三角形,则E的坐标是 .


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com