如果将抛物线y=x²+2向下平移1个单位，那么所得新抛物线的表达式是（　　）

A．y=（x﹣1）²+2       B．y=（x+1）²+2 C．y=x²+1     D．y=x²+3

下列函数中，当x＞0时，y值随x值的增大而减小的是（　　）

A．y=x   B．y=2x﹣1   C．y=   D．y=x²

已知反比例函数y=的图象经过点P（﹣1，2），则这个函数的图象位于（　　）

A．第二，三象限 B．第一，三象限  C．第三，四象限 D．第二，四象限

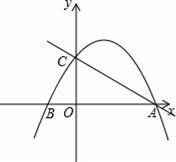
在平面直角坐标系中，已知点B的坐标是（﹣1，0），点A的坐标是（4，0），点C的坐标是（0，4），抛物线过A、B、C三点．

（1）求抛物线的解析式．

（2）点N事抛物线上的一点（点N在直线AC上方），过点N作NG⊥x轴，垂足为G，交AC于点H，当线段ON与CH互相平分时，求出点N的坐标．

（3）设抛物线的对称轴为直线L，顶点为K，点C关于L的对称点J，x轴上是否存在一点Q，y轴上是否一点R使四边形KJQR的周长最小？若存在，请求出周长的最小值；若不存在，请说明理由．

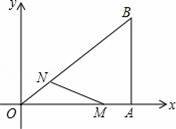
如图，在直角坐标系中，Rt△OAB的直角顶点A在x轴上，OA=4，AB=3．动点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒1.25个单位长度的速度，沿OB向终点B移动．当两个动点运动了x秒（0＜x＜4）时，解答下列问题：

（1）求点N的坐标（用含x的代数式表示）；

（2）设△OMN的面积是S，求S与x之间的函数表达式；当x为何值时，S有最大值？最大值是多少？

（3）在两个动点运动过程中，是否存在某一时刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，请说明理由．

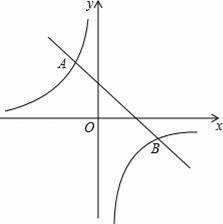
如图：已知反比例函数y=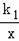与一次函数y=k₂x+b的图象交于A（2，﹣1），B（）．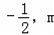

（1）求k₁、k₂，b的值；

（2）求三角形AOB的面积；

（3）若M（x₁，y₁），N（x₂，y₂）是反比例函数y=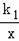图象上的两点，且x₁＜x₂，y₁＞y₂，指出M、N各位于哪个象限，并简单说明理由．

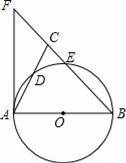
如图，在△ABC中，BA=BC，以AB为直径的⊙O分别交AC、BC于点D、E，BC的延长线于⊙O的切线AF交于点F．

（1）求证：∠ABC=2∠CAF；

（2）若AC=2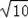，CE：EB=1：4，求CE的长．

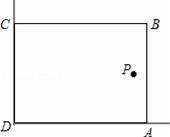
在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm．

（1）若花园的面积为192m²，求x的值；

（2）若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值．

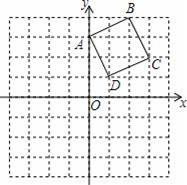
每个小方格都是边长为1个单位长度，正方形ABCD在坐标系中的位置如图所示．

（1）画出正方形ABCD关于原点中心对称的图形；

（2）画出正方形ABCD绕点D点顺时针方向旋转90°后的图形；

（3）求出正方形ABCD的点B绕点D点顺时针方向旋转90°后经过的路线．

 “五•一”假期，某公司组织部分员工分别到A、B、C、D四地旅游，公司按定额购买了前往各地的车票．如图是未制作完的车票种类和数量的条形统计图，根据统计图回答下列问题：

（1）若去D地的车票占全部车票的10%，请求出D地车票的数量，并补全统计图；

（2）若公司采用随机抽取的方式分发车票，每人抽取一张（所有车票的形状、大小、质地完全相同且充分洗匀），那么员工小胡抽到去A地的概率是多少？

（3）若有一张车票，小王、小李都想要，决定采取抛掷一枚各面分别标有1，2，3，4的正四面体骰子的方法来确定，具体规则是：“每人各抛掷一次，若小王掷得着地一面的数字比小李掷得着地一面的数字小，车票给小王，否则给小李”．试用“列表法或画树状图”的方法分析，这个规则对双方是否公平？