
科目: 来源: 题型:
2015年12月北京市中小学雾霾停课期间,学生通过“北京数字学校”等方式实现“停课不停学”.调查结果数据显示,仅8日一天,北京数字学校日访问量达1010000次. 1010000用科学记数法可表示为
A. B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
在平面直角坐标系xOy中,已知直线l的参数方程为 (t为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程是
(t为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程是
(Ⅰ)写出直线l的普通方程与曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A、B两点,求 的值。
的值。
查看答案和解析>>
科目: 来源: 题型:
已知椭圆C的中心在原点,焦点在x轴上,且短轴的长为2,离心率等于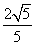 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若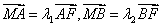 ,求证:
,求证: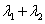 为定值。
为定值。
查看答案和解析>>
科目: 来源: 题型:
某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元。
(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台, )的函数解析式
)的函数解析式 ;
;
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得下表:
| 周需求量n | 18 | 19 | 20 | 21 | 22 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com