
科目: 来源: 题型:
2001年亚洲铁人三项赛在徐州市风光秀丽的云龙湖畔举行.比赛程序是:运动员先同时下水游泳1.5千米到第一换项点,在第一换项点整理服装后,接着骑自行车行40千米到第二换项点,再跑步10千米到终点.下表是2001年亚洲铁人三项赛女子组(19岁以下)三名运动员在比赛中的成绩(游泳成绩即游泳所用时间,其它类推,表内时间单位为秒)
| 运动员号码 | 游泳成绩 | 第一换项点所用时间 | 自行车成绩 | 第二换项点所用时间 | 长跑成绩 |
| 191 | 1997 | 75 | 4927 | 40 | 3220 |
| 194 | 1503 | 110 | 5686 | 57 | 3652 |
| 195 | 1354 | 74 | 5351 | 44 | 3195 |
(1)填空(精确到0.01):
第191号运动员骑自行车的平均速度是 米/秒;
第194号运动员骑自行车的平均速度是 米/秒;
第195号运动员骑自行车的平均速度是 米/秒;
(2)如果运动员骑自行车都是匀速的,那么在骑自行车的途中,191号运动员会追上195号或194号吗?如果会,那么追上时离第一换项点有多少米(精确到0.01)?如果不会,为什么?
(3)如果长跑也都是匀速的,那么在长跑途中这三名运动员中有可能某人追上某人吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.


查看答案和解析>>
科目: 来源: 题型:
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.


查看答案和解析>>
科目: 来源: 题型:
观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….
(1)你能从中推导出计算12+22+32+42+…+n2的公式吗?请写出你的推导过程;
(2)请你用(1)中推导出的公式来解决下列问题:
已知:如图,抛物线y=﹣x2+2x+3与x、y轴的正半轴分别交于点A、B,将线段OAn等分,分点从左到右依次为A1、A2、A3、A4、A5、A6、…、An﹣1,分别过这n﹣1个点作x轴的垂线依次交抛物线于点B1、B2、B3、B4、B5、B6、…、Bn﹣1,设△OBA1、△A1B1A2、△A2B2A3、△A3B3A4、…、△An﹣1Bn﹣1A的面积依次为S1、S2、S3、S4、…、Sn.
①当n=2013时,求s1+s2+s3+s4+…+s2013的值;
②试探究:当n取到无穷无尽时,题中所有三角形的面积和将是什么值?为什么?


查看答案和解析>>
科目: 来源: 题型:
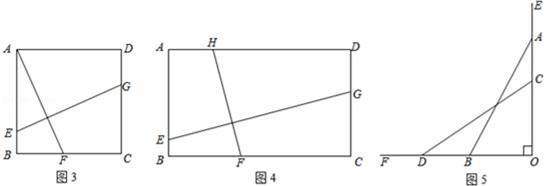
如图1,A、B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)


【问题解决】
如图2,过点B作BB′⊥l2,且BB′等于河宽,连接AB′交l1于点M,作MN⊥l1交l2于点N,则MN就为桥所在的位置.
【类比联想】
(1)如图3,正方形ABCD中,点E、F、G分别在AB、BC、CD上,且AF⊥GE,求证:AF=EG.
(2)如图4,矩形ABCD中,AB=2,BC=x,点E、F、G、H分别在AB、BC、CD、AD上,且EG⊥HF,设y=
 ,试求y与x的函数关系式.
,试求y与x的函数关系式.
【拓展延伸】
如图5,一架长5米的梯子斜靠在竖直的墙面OE上,初始位置时OA=4米,由于地面OF较光滑,梯子的顶端A下滑至点C时,梯子的底端B左滑至点D,设此时AC=a米,BD=b米.
(3)当a= 1 米时,a=b.
(4)当a在什么范围内时,a<b?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
如图1,A、B、C、D为矩形的四个顶点,AD=4cm,AB=dcm.动点E、F分别从点D、B出发,点E以1cm/s的速度沿边DA向点A移动,点F以1cm/s的速度沿边BC向点C移动,点F移动到点C时,两点同时停止移动.以EF为边作正方形EFGH,点F出发xs时,正方形EFGH的面积为ycm2.已知y与x的函数图象是抛物线的一部分,如图2所示.请根据图中信息,解答下列问题:
(1)自变量x的取值范围是 0≤x≤4 ;
(2)d= 3 ,m= 2 ,n= 25 ;
(3)F出发多少秒时,正方形EFGH的面积为16cm2?


查看答案和解析>>
科目: 来源: 题型:
设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的⊙O的圆心O在直线l上运动,点A、O间距离为d.


(1)如图①,当r<a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:
| d、a、r之间关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a﹣r<d<a+r | |
| d=a﹣r | |
| d<a﹣r |
所以,当r<a时,⊙O与正方形的公共点的个数可能有 个;
(2)如图②,当r=a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:
| d、a、r之间关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a≤d<a+r | |
| d<a |
所以,当r=a时,⊙O与正方形的公共点个数可能有 个;
(3)如图③,当⊙O与正方形有5个公共点时,试说明r=
 a.
a.
查看答案和解析>>
科目: 来源: 题型:
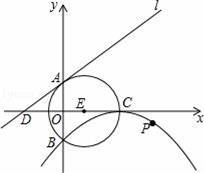
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=
 x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com