
科目: 来源:2014-2015学年四川省成都市外国语学校中考直升模拟数学试卷(解析版) 题型:填空题
双曲线y= (x>0)与直线y=x在坐标系中的图象如图所示,点A、B在直线上AC、BD分别平行y轴,交曲线于C、D两点,若BD=2AC 则4OC2-OD2的值为 .
(x>0)与直线y=x在坐标系中的图象如图所示,点A、B在直线上AC、BD分别平行y轴,交曲线于C、D两点,若BD=2AC 则4OC2-OD2的值为 .

查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市外国语学校中考直升模拟数学试卷(解析版) 题型:解答题
计算题
(1)先化简,再求值: ,其中a=sin45°,b=cos30°;
,其中a=sin45°,b=cos30°;
(2)若关于x的方程 无解,求a的值.
无解,求a的值.
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市外国语学校中考直升模拟数学试卷(解析版) 题型:解答题
如图,梯形ABCD中,AD∥BC,AB=DC,AE⊥BC于点E,AB的垂直平分线GF交BC于点F,交AB于点G,连接AF.已知AD=1.4,AF=5,GF=4.

(1)求梯形ABCD的腰AB的长;
(2)求梯形AFCD的面积.
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市外国语学校中考直升模拟数学试卷(解析版) 题型:解答题
已知点M,N的坐标分别为(0,1),(0,-1),点P是抛物线y= x2上的一个动点.
x2上的一个动点.

(1)求证:以点P为圆心,PM为半径的圆与直线y=-1的相切;
(2)设直线PM与抛物线y= x2的另一个交点为点Q,连接NP,NQ,求证:∠PNM=∠QNM.
x2的另一个交点为点Q,连接NP,NQ,求证:∠PNM=∠QNM.
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市外国语学校中考直升模拟数学试卷(解析版) 题型:解答题
已知,如图,PA是⊙O切线,切点为A,PB交⊙O于C且过圆心O,D是OB中点,连结AB并延长交⊙O于E,若∠APB=30°,AP= ,求AE的长.
,求AE的长.

查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市外国语学校中考直升模拟数学试卷(解析版) 题型:解答题
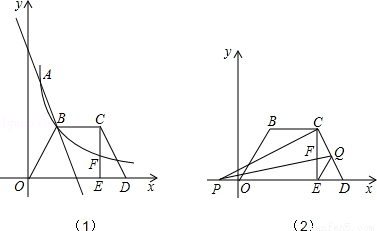
如图(1),直线y=k1 x+b与反比例函数y= 的图象交于点A(1,6),B(a,3)两点.
的图象交于点A(1,6),B(a,3)两点.
(1)求k1、k2的值;
(2)如图(1),等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点F,当梯形OBCD的面积为12时,请判断FC和EF的大小,并说明理由;
(3)如图(2),已知点Q是CD的中点,在第(2)问的条件下,点P在x轴上,从原点O出发,沿x轴负方向运动,设四边形PCQE的面积为S1,△DEQ的面积为S2,当∠PCD=90°时,求P点坐标及S1:S2的值.
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市外国语学校中考直升模拟数学试卷(解析版) 题型:解答题
研究所对某种新型产品的产销情况进行了研究,为投资商在甲、乙两地生产并销售该产品提供了如下成果:第一年的年产量为x(吨)时,所需的全部费用y(万元)与x满足关系式y= x2+5x+90,
x2+5x+90,
投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲、p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)
(1)成果表明,在甲地生产并销售x吨时,p甲=- x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;
x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;
(2)成果表明,在乙地生产并销售x吨时,p乙=- x+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
x+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
(3)受资金、生产能力等多种因素的影响,某投资商计划第一年生产并销售该产品18吨,根据(1)、(2)中的结果,请你通过计算帮他决策,选择在甲地还是乙地产销才能获得最大的年利润?
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市外国语学校中考直升模拟数学试卷(解析版) 题型:解答题
阅读以下材料:
对于三个数a、b、c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}= ;min{-1,2,3}=-1,…解决下列问题:
;min{-1,2,3}=-1,…解决下列问题:
(1)填空:如果min{2,2x+2,4-2x}=2,则x的取值范围为 ;
(2)①如果M{2,x+1,2x}=min{2,x+1,2x},求x;
②根据①,你发现了结论:如果M{a,b,c}=min{a,b,c},那么 (填a、b、c的大小关系),证明你发现的结论.
③运用②的结论,填空:若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,+2x-y,则x+y=
(3)在同一直角坐标系中作出函数y=x+1,y=(x-1)2,y=2-x的图象(不需列表描点),通过观察图象,填空:min{x+1,(x-1)2,2-x}的最大值为 .
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市外国语学校中考直升模拟数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B、C,与y轴的负半轴相交于D.

(1)若抛物线y=ax2+bx+c经过B、C、D三点,求此抛物线的解析式,并写出抛物线与圆A的另一个交点E的坐标;
(2)若动直线MN(MN∥x轴)从点D开始,以每秒1个长度单位的速度沿y轴的正方向移动,且与线段CD、y轴分别交于M、N两点,动点P同时从点C出发,在线段OC上以每秒2个长度单位的速度向原点O运动,连接PM,设运动时间为t秒,当t为何值时, 的值最大,并求出最大值;
的值最大,并求出最大值;
(3)在(2)的条件下,若以P、C、M为顶点的三角形与△OCD相似,求实数t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com