
科目: 来源:2014-2015学年广东省广州市毕业班综合测试数学试卷(解析版) 题型:解答题
如图,AB为⊙O的直径,劣弧 ,BD∥CE,连接AE并延长交BD于D.求证:
,BD∥CE,连接AE并延长交BD于D.求证:

(1)AC=AE;
(2)AB2=AC•AD.
查看答案和解析>>
科目: 来源:2014-2015学年广东省广州市毕业班综合测试数学试卷(解析版) 题型:解答题
为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:

(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
查看答案和解析>>
科目: 来源:2014-2015学年广东省广州市毕业班综合测试数学试卷(解析版) 题型:解答题
如图所示,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数y=- 的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.
的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.

(1)求直线AB的解析式;
(2)若点P是线段BD上一点,且△PBC的面积等于3,求点P的坐标.
查看答案和解析>>
科目: 来源:2014-2015学年广东省广州市毕业班综合测试数学试卷(解析版) 题型:解答题
为顺利通过“国家文明城市”验收,东营市政府拟对城区部分路段的人行道地砖、绿化带、排水管道等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
查看答案和解析>>
科目: 来源:2014-2015学年广东省广州市毕业班综合测试数学试卷(解析版) 题型:解答题
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.

(1)动手操作:利用尺规作⊙O,使⊙O经过点A、D,且圆心O在AB上;并标出⊙O与AB的另一个交点E(保留作图痕迹,不写作法);
(2)综合应用:在你所作的图中,
①判断直线BC与⊙O的位置关系,并说明理由;
②若AB=6,BD=2 ,求线段BD、BE与劣弧
,求线段BD、BE与劣弧 所围成的图形面积(结果保留根号和π).
所围成的图形面积(结果保留根号和π).
查看答案和解析>>
科目: 来源:2014-2015学年广东省广州市毕业班综合测试数学试卷(解析版) 题型:解答题
如图,抛物线y=-x2+bx+c的顶点为D,与x轴交于A(-1,0)、B(3,0),与y轴交于点C.
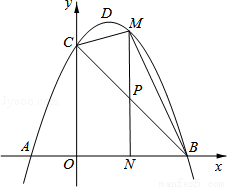
(1)求该抛物线的解析式;
(2)若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当四边形OBMC的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当四边形OBMC的面积最大时,在抛物线的对称轴上是否存在点Q,使得△CNQ为直角三角形?若存在,直接写出点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com