(1)计算：

(2)解不等式组：

先化简，再求值：，其中x=＋2．

如图，在□ABCD中，E、F为BC上的两点，且BE=CF，AF=DE.求证：

（1）△ABF≌△DCE；

（2）四边形ABCD是矩形.

甲、乙两商场同时开业，为了吸引顾客，都举办有奖酬宾活动，凡购物满100元，均可得到一次摸奖的机会．在一个纸盒里装有2个红球和2个白球，除颜色外，其他全部相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券的多少（如下表）．

（1）请你用列表法（或画树状图）求出摸到一红一白的概率；

（2）如果只考虑中奖因素，你将会选择去哪个商场购物？请说明理由．

为了更好地了解某区近阶段九年级学生的中考目标，某研究机构设计了如下调查问卷（单选）：你的中考目标是哪一个？

A．升入四星普通高中；B．升入三星级普通高中；C．升入五年制高职类学校； D．升入中等职业类学校；E．等待初中毕业，不想再读书了．

在随机调查了某区3000名九年级学生中的部分学生后，统计整理并制作了如下的统计图．根据有关信息解答下列问题：

（1）此次共调查了 名学生，计算扇形统计图中= ．

(2) 补全条形统计图。

(3) 请你估计其中有多少名学生选择升入四星普通高中。

如图，一艘潜艇在海面下500米深处的A点，测得正前方俯角为31.0°方向上的海底有黑匣子发出的信号，潜艇在同一深度保持直线航行500米，在B点处测得海底黑匣子位于正前方俯角为36.9°的方向上，求海底黑匣子C所在点距离海面的深度．（精确到1米）（参考数据：sin36.9° ≈ 0.60，cos36.9° ≈ 0.80，tan36.9° ≈0.75，sin31.0°≈ 0.51，cos31.0°≈0.87 ，tan31.0°≈ 0.60）

如图，一次函数的图象与x轴、y轴分别相交于A、B两点，且与反比例函数y=（k≠0）的图象在第一象限交于点C，如果点B的坐标为（0，2），OA=OB，B是线段AC的中点．

（1）求点A的坐标及一次函数解析式．

（2）求点C的坐标及反比例函数的解析式．

某批发商以40元/千克的成本价购入了某产品700千克，据市场预测，该产品的销售价y（元/千克）与保存时间x（天）的函数关系为y=50+2x，但保存这批产品平均每天将损耗15千克，且最多保存15天．另外，批发商每天保存该批产品的费用为50元．

（1）若批发商在保存该产品5天时一次性卖出，则可获利 元．

（2）如果批发商希望通过这批产品卖出获利10000元，则批发商应在保存该产品多少天时一次性卖出？

如图1，在Rt△ACB中，∠ACB=90°，AC=3，BC=4，有一过点C的动圆⊙O与斜边AB相切于动点P，连接CP．

（1）当⊙O与直角边AC相切时，如图2所示，求此时⊙O的半径r的长；

（2）随着切点P的位置不同，弦CP的长也会发生变化，试求出弦CP的长的取值范围．

（3）当切点P在何处时，⊙O的半径r有最大值？试求出这个最大值．

如图，⊙E的圆心E(3，0)，半径为5，⊙E与y轴相交于A、B两点(点A在点B的上方)，与x轴的正半轴相交于点C；直线l的解析式为y=x＋4，与x轴相交于点D；以C为顶点的抛物线经过点B.

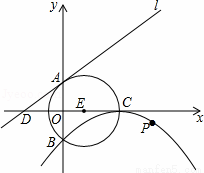
(1)求抛物线的解析式；

(2)判断直线l与⊙E的位置关系，并说明理由；

(3) 动点P在抛物线上，当点P到直线l的距离最小时，求出点P的坐标及最小距离.