
科目: 来源:2016年初中毕业升学考试(辽宁大连卷)数学(解析版) 题型:填空题
如图,抛物线y=ax2+bx+c与x轴相交于点A、B(m+2,0)与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是 .

查看答案和解析>>
科目: 来源:2016年初中毕业升学考试(辽宁大连卷)数学(解析版) 题型:解答题
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>4.0 | 3 |
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有 户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为 户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在 组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.

查看答案和解析>>
科目: 来源:2016年初中毕业升学考试(辽宁大连卷)数学(解析版) 题型:解答题
A、B两地相距200千米,甲车从A地出发匀速开往B地,乙车同时从B地出发匀速开往A地,两车相遇时距A地80千米.已知乙车每小时比甲车多行驶30千米,求甲、乙两车的速度.
查看答案和解析>>
科目: 来源:2016年初中毕业升学考试(辽宁大连卷)数学(解析版) 题型:解答题
如图,抛物线y=x2﹣3x+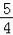 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
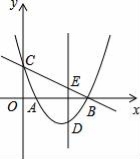
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
查看答案和解析>>
科目: 来源:2016年初中毕业升学考试(辽宁大连卷)数学(解析版) 题型:解答题
如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC

(1)求证:DE与⊙O相切;
(2)若BF=2,DF= ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目: 来源:2016年初中毕业升学考试(辽宁大连卷)数学(解析版) 题型:解答题
如图1,△ABC中,∠C=90°,线段DE在射线BC上,且DE=AC,线段DE沿射线BC运动,开始时,点D与点B重合,点D到达点C时运动停止,过点D作DF=DB,与射线BA相交于点F,过点E作BC的垂线,与射线BA相交于点G.设BD=x,四边形DEGF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤m,1<x≤m,m<x≤3时,函数的解析式不同)
(1)填空:BC的长是 ;
(2)求S关于x的函数关系式,并写出x的取值范围.

查看答案和解析>>
科目: 来源:2016年初中毕业升学考试(辽宁大连卷)数学(解析版) 题型:解答题
阅读下面材料:
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k< ),∠AED=∠BCD,求
),∠AED=∠BCD,求 的值(用含k的式子表示).
的值(用含k的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com