练习册

  • 练习册
  • 试题
    相关习题
     0  278161  278169  278175  278179  278185  278187  278191  278197  278199  278205  278211  278215  278217  278221  278227  278229  278235  278239  278241  278245  278247  278251  278253  278255  278256  278257  278259  278260  278261  278263  278265  278269  278271  278275  278277  278281  278287  278289  278295  278299  278301  278305  278311  278317  278319  278325  278329  278331  278337  278341  278347  278355  366461 

    科目： 来源： 题型：选择题

    18．用下列哪种方法解方程3（x-2）2=2x-4比较简便（　　）
    A．直接开平方法B．配方法C．公式法D．因式分解法

    查看答案和解析>>

    科目： 来源： 题型：解答题

    17．如图，△ABC的面积为4cm2，周长为10cm，求△ABC的内切圆半径．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．解方程：
    （1）x2-3x+1=0
    （2）x2-3x=0
    （3）x2-2x=4．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    15．如图，直角三角形斜边长为12，内切圆的半径为1，求三角形的周长．

    查看答案和解析>>

    科目： 来源： 题型：解答题

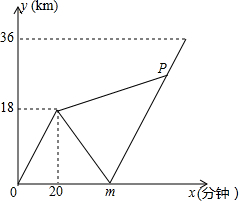    14．甲、乙两名大学生去距学校36千米的某乡镇进行社会调查，他们从学校出发，骑电动车行驶20分钟时发现忘带相机，甲下车前往，乙骑电动车按原路返回，乙取相机后（在学校取相机所用时间忽略不计）骑电动车追甲．在距乡镇13.5千米处追上甲后同车前往乡镇．乙电动车的速度始终不变．设甲与学校相距y甲（千米），乙与学校相离y乙（千米），甲离开学校的时间为x（分钟）．y甲、y乙与x之间的函数图象如图所示，结合图象解答下列问题：
    （1）电动车的速度为0.9千米/分钟；
    （2）m的值为40；
    （3）求乙取到相机后从学校返回发到达目的地时y乙与x之间的函数关系式；
    （4）求点P的坐标，并解释点P的意义；
    （5）求乙返回到学校时，甲与学校相距多远？

    查看答案和解析>>

    科目： 来源： 题型：解答题

    13．如图所示，在Rt△ABC中，∠C=90°，BC=3，AC=4，⊙O与边AB，BC，AC分别相切于点E，F，G．求⊙O的半径．

    查看答案和解析>>

    科目： 来源： 题型：填空题

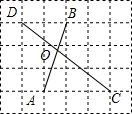    12．如图，在每个单位格线长为1的网格图中，A、B、C、D是四个格点，AB、CD相交于点O．则OD=2；△AOC的面积=$\frac{9}{10}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    11．解方程组：
    （1）$\left\{\begin{array}{l}{x+2y=10}\\{y=2x}\end{array}\right.$
    （2）$\left\{\begin{array}{l}{2x+3y=7}\\{x-3y=8}\end{array}\right.$　
    （3）$\left\{\begin{array}{l}{\frac{2（x-y）}{3}+1=\frac{x+y}{4}}\\{3（x+y）-2（2x-y）=8}\end{array}\right.$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

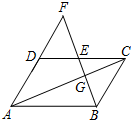    10．如图，?ABCD中，E是边CD的中点，连结BE并延长，交AD的延长线于点F．
    （1）求证：EF=EB；
    （2）连结AC，交BF于点G，若EG=2，求EF的长．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    9．定义：如果二次函数y=ax2+bx+c的图象经过点（-1，0），那么称此二次函数图象为“线性曲线”．例如：二次函数y=2x2-5x-7和y=-x2+3x+4的图象都是“线性曲线”．若“线性曲线”y=x2-mx+1-2k与坐标轴只有两个公共点，则k的值0或$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案