5．如图.在△ABC中.AD⊥BC于D.CE平分∠ACB分别交AB.AD于E.F两点.且BD=FD.AB=CF．求证:AE=BE．——青夏教育精英家教网—

相关习题

0 278196 278204 278210 278214 278220 278222 278226 278232 278234 278240 278246 278250 278252 278256 278262 278264 278270 278274 278276 278280 278282 278286 278288 278290 278291 278292 278294 278295 278296 278298 278300 278304 278306 278310 278312 278316 278322 278324 278330 278334 278336 278340 278346 278352 278354 278360 278364 278366 278372 278376 278382 278390 366461

科目： 来源： 题型：解答题

5．

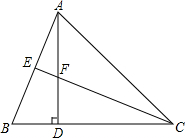如图，在△ABC中，AD⊥BC于D，CE平分∠ACB分别交AB、AD于E、F两点，且BD=FD，AB=CF．求证：（1）CE⊥AB；（2）AE=BE．

查看答案和解析>>

科目： 来源： 题型：解答题

4．计算${（{-\frac{a}{b}}）^2}•{（{\frac{b}{a^2}}）^2}÷{（{-2ab}）^2}$．

查看答案和解析>>

科目： 来源： 题型：解答题

3．（1）a⁴-a²b²
（2）4x³+4x²y+xy²
（3）x²+4x-21
（4）x²-y²+2y-1．

查看答案和解析>>

科目： 来源： 题型：解答题

2．定义：直线y=ax+b（a≠0）称作抛物线y=ax²+bx（a≠0）的关联直线．根据定义回答以下问题：
（1）已知抛物线y=ax²+bx（a≠0）的关联直线为y=x+2，则该抛物线的顶点坐标为（-1，-1）；
（2）求证：抛物线y=ax²+bx与其关联直线一定有公共点；
（3）当a=1时，请写出抛物线y=ax²+bx与其关联直线所共有的特征（写出一条即可）．

查看答案和解析>>

科目： 来源： 题型：解答题

1．

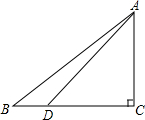如图，在Rt△ABC中，∠C=90°，sin=$\frac{3}{5}$，点D在BC边上，DC=AC=6．
（1）求AB的值；
（2）求tan∠BAD的值．

查看答案和解析>>

科目： 来源： 题型：解答题

20．计算：sin30°-$\sqrt{2}$sin45°+tan60°•cos30°．

查看答案和解析>>

科目： 来源： 题型：填空题

19．

北京紫禁城是中国古代汉族宫廷建筑之精华．经测算发现，太和殿，中和殿，保和殿这三大殿的矩形宫院ABCD（北至保和殿，南至太和门，西至弘义阁，东至体仁阁）与三大殿下的工字形大台基所在的矩形区域EFGH为相似形．若比较宫院与台基之间的比例关系，可以发现接近于9：5，取“九五至尊”之意．根据测量数据，三大殿台基的宽为40丈，请你估算三大殿宫院的宽为72丈．

查看答案和解析>>

科目： 来源： 题型：解答题

18．

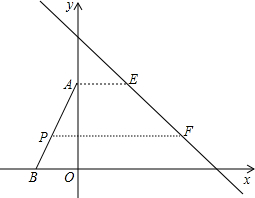如图，△ABO的顶点A、B的坐标分别为（0，4）、（-2，0），直线l交x轴于C、交y轴于D，且它所对应的函数表达式为y=-x+6；规定：对于平面上的某一点M，当它沿水平向右的方向平移，平移到直线l上为止，这个过程中平移的距离，称为点M的“右平移距离”．
（1）请你直接写出D点坐标、A点的“右平移距离”（AE的长度）、直线AB的表达式；
（2）若线段AB上有一点P的“右平移距离”PF=6，试求出P点的坐标；
（3）若某点的“右平移距离”不超过6，则称该点为“安全点”．在△ABO的内部或边上的所有“安全点”集中在一定的区域，试求出这个区域的面积．

查看答案和解析>>

科目： 来源： 题型：填空题

17．

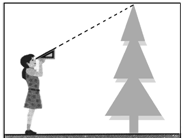小莉站在离一棵树水平距离为2米的地方，用一块含30°的直角三角板按如图所示的方式测量这棵树的高度，已知小莉的眼睛离地面的高度是1.5米，那么她测得这棵树的高度为（$\frac{2\sqrt{3}}{3}$+1.5）米．（结果保留根号）