
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
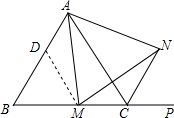 如图,在等边三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
如图,在等边三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.
如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.查看答案和解析>>
科目: 来源: 题型:解答题
 我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.
我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.查看答案和解析>>
科目: 来源: 题型:填空题
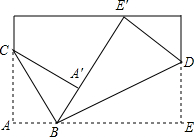 同学们,你玩过折纸游戏吗?折纸游戏里还蕴藏着不少数学知识呢!请准备一张长方形纸片,按照小亮的方法折纸,折叠后A′B与E′B在同一直线上,如图所示,则两折痕BC与BD的夹角∠CBD的度数为90°.
同学们,你玩过折纸游戏吗?折纸游戏里还蕴藏着不少数学知识呢!请准备一张长方形纸片,按照小亮的方法折纸,折叠后A′B与E′B在同一直线上,如图所示,则两折痕BC与BD的夹角∠CBD的度数为90°.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com