
科目: 来源: 题型:选择题
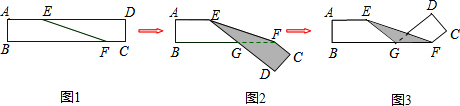
| A. | 27° | B. | 26° | C. | 23° | D. | 22° |
查看答案和解析>>
科目: 来源: 题型:填空题
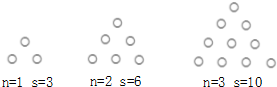 如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.
如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
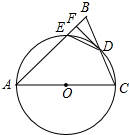 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.查看答案和解析>>
科目: 来源: 题型:解答题
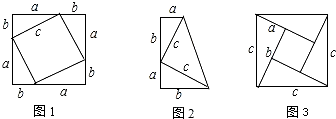
查看答案和解析>>
科目: 来源: 题型:解答题
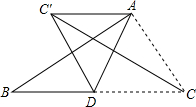 如图,AD是△ABC的边BC上的中线,且AD=BD=CD,把△ADC沿AD对折,点C落在点C′处,连接CC′,图中有哪些线段互相垂直?请一一写出来,并选择其中一组加以证明.
如图,AD是△ABC的边BC上的中线,且AD=BD=CD,把△ADC沿AD对折,点C落在点C′处,连接CC′,图中有哪些线段互相垂直?请一一写出来,并选择其中一组加以证明.查看答案和解析>>
科目: 来源: 题型:解答题
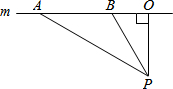 随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.
随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com