6．如图，在Rt△ABC中，∠C=90°，AC=8cm，BC=6cm，点P以1cm/s的速度从A开始沿着折线AB-BC运动到点C，点D在AC上，连接BD，PD，设点P的运动时间为t秒；
（1）直接写出AB的长度；
（2）把△BCD沿着BD对折，点C恰好落在AB上的点E处，求此时CD的长；
（3）若点D在（2）中的位置，当t为几秒时，△BPD为直角三角形？

5．如图，等腰直角△ABC腰长为10，现分别按图1、图2方式在△ABC内裁剪一个内接正方形ADFE和正方形PMNQ．设正方形ADFE的面积为S₁，正方形PMNQ的面积为S₂，
（1）在图1 中，求AD：AB的值；在图2中，求AP：AB的值；
（2）比较S₁和S₂的大小，判断哪种裁剪方式所得正方形面积大．

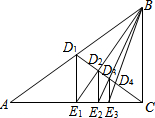4．如图，已知Rt△ABC，D₁是斜边AB的中点，过D₁作D₁E₁⊥AC于E₁，连结BE₁交CD₁于D₂；过D₂作D₂E₂⊥AC于E₂，连结BE₂交CD₁于D₃；过D₃作D₃E₃⊥AC于E₃，…，如此继续，可以依次得到点D₄，D₅，…，D_n，分别记△BD₁E₁，△BD₂E₂，△BD₃E₃，…，△BD_nE_n的面积为S₁，S₂，S₃，…S_n．若S_△ABC=1，则S₂₀₁₀=$\frac{1}{201{1}^{2}}$．

3．如图，在△ABD和△AEC中，E为AD上一点，若∠DAC=∠B，∠AEC=∠BDA．求证：AE•AB=AC•BD．

2．我们定义：“四个顶点都在三角形边上的正方形是三角形的内接正方形”．
已知：在Rt△ABC中，∠C=90°，AC=6，BC=3．
（1）如图1，四边形CDEF是△ABC的内接正方形，则正方形CDEF的边长a₁是2；
（2）如图2，四边形DGHI是（1）中△EDA的内接正方形，则第2个正方形DGHI的边长a₂=$\frac{4}{3}$．

1．方程5x²=6x-8化成一元二次方程一般形式后，二次项系数、一次项系数、常数项分别是5、-6、8．

20．已知二次函数y=2x²-4x-6．
（1）求出该函数与x轴的交点坐标（-1，0）、（3，0）；与y轴的交点坐标（0，-6）；
（2）在平面直角坐标系中，用描点法画出这个二次函数的图象；
（3）当y＞0时，则x的取值范围是x＜-1或x＞3．

19．学校要围一个矩形花圃，其一边利用足够长的墙，另三边用篱笆围成，由于园艺需要，还要用一段篱笆将花圃分隔为两个小矩形部分（如图所示），总共36米的篱笆恰好用完（不考虑损耗）．设矩形垂直于墙面的一边AB的长为x米（要求AB＜AD），矩形花圃ABCD的面积为S平方米．
（1）求S与x之间的函数关系式，并直接写出自变量x的取值范围；
（2）要想使矩形花圃ABCD的面积最大，AB边的长应为多少米？

18．如图，在等边△ABC中，D，E，F分别为边AB，BC，CA上的点，且满足∠DEF=60°．
（1）求证：BE•CE=BD•CF；
（2）若DE⊥BC且DE=EF，求$\frac{BE}{EC}$的值．

17．我校九年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作，已知该水果的进价为8元/千克，下面是他们在活动结束后的对话．
小丽：如果以10元/千克的价格销售，那么每天可售出200千克．
小强：如果以12元/千克的价格销售，那么每天可获取利润600元．
小红：通过调查验证，我发现每天的销售量y（千克）与销售单价x（元）之间存在一次函数关系．
（1）求y（千克）与x（元）（x＞0）的函数关系式；
（2）当销售单价为何值时，该超市销售这种水果每天获取的利润达到525元？
[利润=销售量×（销售单价-进价）]
（3）一段时间后，发现这种水果每天的销售量均不低于225千克．则此时该超市销售这种水果每天获取的利润最大值是多少？