
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
 已知:如图,在梯形ABCD中,AD∥BC,AD=$\frac{1}{3}BC$,点M是边BC的中点$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$
已知:如图,在梯形ABCD中,AD∥BC,AD=$\frac{1}{3}BC$,点M是边BC的中点$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$查看答案和解析>>
科目: 来源: 题型:解答题
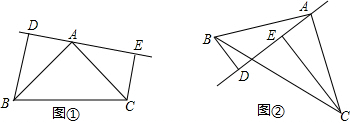
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:填空题
 如图,四边形ABCD中,AB∥CD,点E是边AD上的点,BE平分∠ABC,CE平分∠BCD,有下列结论:①AD=AB+CD,②E为AD的中点,③BC=AB+CD,④BE⊥CE,其中正确的有②③④.(填序号)
如图,四边形ABCD中,AB∥CD,点E是边AD上的点,BE平分∠ABC,CE平分∠BCD,有下列结论:①AD=AB+CD,②E为AD的中点,③BC=AB+CD,④BE⊥CE,其中正确的有②③④.(填序号)查看答案和解析>>
科目: 来源: 题型:解答题
 小东同学在学习了二次函数图象以后,自己提出了这样一个问题:
小东同学在学习了二次函数图象以后,自己提出了这样一个问题:| x | … | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | 4 | … |
| y | … | $\frac{25}{6}$ | $\frac{3}{2}$ | $-\frac{1}{2}$ | $-\frac{15}{8}$ | $-\frac{53}{18}$ | $\frac{55}{18}$ | $\frac{17}{8}$ | $\frac{3}{2}$ | $\frac{5}{2}$ | m | … |
查看答案和解析>>
科目: 来源: 题型:解答题
 (1)操作发现 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(1)操作发现 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.查看答案和解析>>
科目: 来源: 题型:解答题
 已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com