科目： 来源： 题型：填空题

16．如图，观察下列图形中三角形个数变化规律，那么第n个图形中一共有4n-3个三角形（用含字母n的代数式表示）．

科目： 来源： 题型：选择题

15．如图，五角星绕着它的旋转中心旋转，使得△ABC与△DEF重合，那么旋转角的度数至少为（　　）

A．

60°

B．

120°

C．

72°

D．

144°

科目： 来源： 题型：解答题

14．一辆货车从甲地开往乙地，一辆客车从乙地开往甲地，客车先出发45分钟后，货车出发．如图是货车和客车离甲地的距离y_货、y_客（km）与货车行驶的时间x（h）之间的函数关系图象，根据图象回答下列问题：
（1）直接写出：甲、乙两地相距300km，货车比客车晚2h到达终点
（2）货车出发几小时两车相遇？
（3）客车出发几小时，两车相距100km？

科目： 来源： 题型：解答题

13．如图①，在Rt△ACB中，∠ACB=90°，∠ABC=30°，AC=1，点D为AC上一动点，连接BD，以BD为边作等边△BDE，设CD=n．
（1）当n=1时，EA的延长线交BC的延长线于F，则AF=2；
（2）当0＜n＜1时，如图②，在BA上截取BH=AD，连接EH．
①设∠CBD=x，用含x的式子表示∠ADE和∠ABE．
②求证：△AEH为等边三角形．

科目： 来源： 题型：解答题

12．如图，四边形ABCD中，∠DAB=∠ABC=90°，AB=BC，E是AB的中点，CE⊥BD．
（1）求证：BE=AD；
（2）求证：AC是线段ED的垂直平分线；
（3）△DBC是等腰三角形吗？并说明理由．

科目： 来源： 题型：解答题

11．已知Rt△ABC中，AC=BC，∠C=90°，D为AB边的中点，∠EDF=90°，如图①∠EDF的两边分别交AC、CB（或它们的延长线）于E、F．当∠EDF的边DE⊥AC于E时，S_△DEF，S_△CEF，S_△ABC满足S_△DEF+S_△CEF=$\frac{1}{2}$S_△ABC；
（1）如图②，当∠EDF的边DE和AC不垂直时，请证明上述结论仍然成立；
（2）如图③，当∠EDF的边DE与AC的延长线交于点E的情况下，上述结论是否成立？若成立，请给予证明；若不成立，S_△DEF，S_△CEF，S_△ABC，又有怎样的数量关系？请写出你的猜想，不需证明．

科目： 来源： 题型：填空题

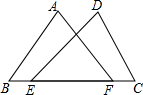10．如图，点E，F在BC边上，AB=DC，∠B=∠C．要使得∠A=∠D．则可以添加的条件是∠AFE=∠DEF或BF=CE或BE=CF（答案不唯一）（写一个即可）．

科目： 来源： 题型：选择题

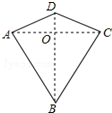9．两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，小明在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO=CO=$\frac{1}{2}$AC；③△ABD≌△CBD，其中正确的结论有（　　）

A．

①②

B．

①③

C．

②③

D．

①②③

科目： 来源： 题型：解答题

8．面积法是解决数学问题的重要方法之一，请结合面积法完成下面问题：
（1）利用图1所示图形的面积，可说明的数学公式为（a+b）²=a²+2ab+b²；
（2）利用图2所示图形的面积，可说明的数学公式为a²-b²=（a+b）（a-b）；
（3）请结合图3中所给出的正方形，利用面积法说明完全平方差公式．

科目： 来源： 题型：解答题

7．如图：在△ABC中，点D在AB边上，点E在AC边的延长线上，CE=BD，DG=GE．求证：AB=AC．