
科目: 来源: 题型:解答题
 直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y=$\frac{m}{x}$(x<0)交于点A(-1,n).
直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y=$\frac{m}{x}$(x<0)交于点A(-1,n).查看答案和解析>>
科目: 来源: 题型:填空题
| 特殊网图 |  |  |  |  |
| 结点数(V) | 4 | 6 | 9 | 12 |
| 网眼数(F) | 1 | 2 | 4 | 6 |
| 边数(E) | 4 | 7 | 12 | ☆ |

查看答案和解析>>
科目: 来源: 题型:解答题
 在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.
在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.查看答案和解析>>
科目: 来源: 题型:解答题
 小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.
小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,某市对位于笔直公路上的两个小区A、B的供水路线进行优化改造,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区B到供水站M的距离为300米,
如图,某市对位于笔直公路上的两个小区A、B的供水路线进行优化改造,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区B到供水站M的距离为300米,查看答案和解析>>
科目: 来源: 题型:解答题
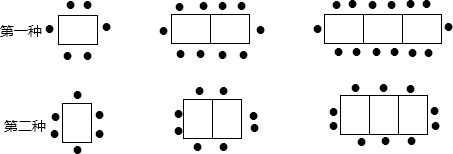
查看答案和解析>>
科目: 来源: 题型:填空题

查看答案和解析>>
科目: 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,四边形是正方形,BM=DF,AF垂直AM,点M、B、C在一条直线上,且△AEM与△AEF恰好关于所在直线成轴对称.已知EF=x,正方形边长为y.
如图,四边形是正方形,BM=DF,AF垂直AM,点M、B、C在一条直线上,且△AEM与△AEF恰好关于所在直线成轴对称.已知EF=x,正方形边长为y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com