7．如图①，在平面直角坐标系中，直线y=-$\frac{1}{2}$x+6与x轴交于点A，与直线y=x交于点B，沿M为线段OA的中点，C、D两点同时从点M出发，均以每秒1个单位的速度沿x轴分别向终点O、A运动，以CD为边向上作正方形CDEF，设C、D两点运动的t（s）（t＞0）．
（1）点B的坐标为（4，4），△ABO的面积为24；
（2）当点E落在直线y=-$\frac{1}{2}$x+6上时，求t的值；在运动过程中，点F能否与点B重合，请通过计算进行说明；
（3）设正方形CDEF与△ABO重叠部分图形的面积为S，当重叠部分图形为五边形时，求S与t的函数关系式，并写出t的取值范围；
（4）如图②，在点C、D的运动过程中作点B关于直线EF、CF的对称点G、H，请直接写出以BG、BH为邻边的矩形与正方形CDEF重叠部分的面积小于$\frac{9}{8}$时t的取值范围．

6．如图，a∥b，∠1=∠2，∠3=40°，则∠4等于70度．

5．如图，抛物线y=ax²+bx+3与x轴相交于点A（-3，0），B（-1，0），与y轴相交于点C，⊙O₁为△ABC的外接圆，交抛物线于另一点D．
（1）求抛物线的解析式；
（2）求⊙O₁的半径．

4．射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

	第一次	第二次	第三次	第四次	第五次	第六次	平均成绩	中位数
甲	10	8	9	8	10	9	9	①
乙	10	7	10	10	9	8	②	9.5

（1）完成表中填空①9；②9；
（2）请计算甲六次测试成绩的方差；
（3）若乙六次测试成绩方差为$\frac{4}{3}$，你认为推荐谁参加比赛更合适，请说明理由．

3．如图，在平面直角坐标系xOy中，菱形ABCD的顶点A的坐标为（2，0），点B的坐标为（0，1），点C在第一象限，对角线BD与x轴平行．直线y=x+4与x轴、y轴分别交于点E，F．将菱形ABCD沿x轴向左平移k个单位，当点C落在△EOF的内部时（不包括三角形的边），k的值可能是（　　）

A．

2

B．

3

C．

4

D．

5

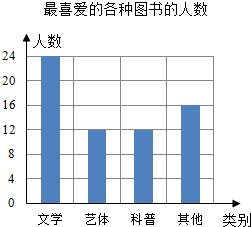2．某校“放飞梦想”读书小组协助老师随机抽取本校的部分学生，调查他们最喜爱的图书类别（图书分为文学类、艺体类、科普类、其他等四类），并将调查结果绘制成如图所示的条形统计图，则被调查的学生中喜爱文学类、艺体类、科普类的共有48人．

1．如图：在平面直角坐标系xOy中，已知正比例函数y=$\frac{4}{3}x$与一次函数y=-x+7的图象交于点A．
（1）求点A的坐标；
（2）在y轴上确定点M，使得△AOM是等腰三角形，请直接写出点M的坐标；
（3）如图、设x轴上一点P（a，0），过点P作x轴的垂线（垂线位于点A的右侧），分别交y=$\frac{4}{3}x$和y=-x+7的图象于点B、C，连接OC，若BC=$\frac{14}{5}$OA，求△ABC的面积及点B、点C的坐标；
（4）在（3）的条件下，设直线y=-x+7交x轴于点D，在直线BC上确定点E，使得△ADE的周长最小，请直接写出点E的坐标．

20．已知直线l₁：y=-$\frac{3}{4}x+3$与直线l₂：y=kx-$\frac{16}{3}$交于x轴上的同一个点A，直线l₁与y轴交于点B，直线l₂与y轴的交点为C．
（1）求k的值，并作出直线l₂图象；
（2）若点P是线段AB上的点且△ACP的面积为15，求点P的坐标；
（3）若点M、N分别是x轴上、线段AC上的动点（点M不与点O重合），是否存在点M、N，使得△ANM≌△AOC？若存在，请求出N点的坐标；若不存在，请说明理由．

19．如图，一次函数y=-kx+n（k≠0）与x轴、y轴分别交于A、B两点，与反比例函数y=$\frac{k}{x}$（k≠0）交于C、D两点，且C、D两点分别是线段AB的三等分点，若S_△AOB=$\frac{9}{4}$，则n=（　　）

A．

-$\sqrt{2}$

B．

-$\frac{3}{2}\sqrt{2}$

C．

-2$\sqrt{2}$

D．

-$\frac{5}{2}\sqrt{2}$

18．如图是二次函数y=ax²+bx+c图象的一部分，图象过点A（-3，0），对称轴为直线x=-1．给出四个结论：①b²＞4ac；②b=-2a；③a+b+c=0；④c-a＞0，其中正确结论的番号是①④．