
科目: 来源: 题型:解答题
 如图,AB为⊙O的弦,D为AB上一点,且OD⊥OB,直线l⊥OA,且直线l与OA的延长线交于点A′,与BA的延长线交于点E,与OD的延长线交于点C′.
如图,AB为⊙O的弦,D为AB上一点,且OD⊥OB,直线l⊥OA,且直线l与OA的延长线交于点A′,与BA的延长线交于点E,与OD的延长线交于点C′.查看答案和解析>>
科目: 来源: 题型:填空题
 如图,四边形ABCD是边长为5的正方形,点G是BC上的一点,DE⊥AG于点E,BF∥DE,且交AG于点F.若E是AF的中点,则BF的长为$\sqrt{5}$.
如图,四边形ABCD是边长为5的正方形,点G是BC上的一点,DE⊥AG于点E,BF∥DE,且交AG于点F.若E是AF的中点,则BF的长为$\sqrt{5}$.查看答案和解析>>
科目: 来源: 题型:解答题
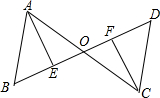 学了三角形全等的知识后,老师提出了一个问题.如图所示,点E、F在线段BD上,线段AC与BD互相平分,且BE=DF.那么△AOE和△COF全等吗?△AOB和△COD全等吗?请说明理由.
学了三角形全等的知识后,老师提出了一个问题.如图所示,点E、F在线段BD上,线段AC与BD互相平分,且BE=DF.那么△AOE和△COF全等吗?△AOB和△COD全等吗?请说明理由.查看答案和解析>>
科目: 来源: 题型:解答题
 如图所示,△ABC为等腰三角形,∠BAC=90°,AD=AE,AF⊥BE交BC于点F,过F作FG⊥CD交BE延长线于G,GF与AC于M,求证:BG=AF+FG.
如图所示,△ABC为等腰三角形,∠BAC=90°,AD=AE,AF⊥BE交BC于点F,过F作FG⊥CD交BE延长线于G,GF与AC于M,求证:BG=AF+FG.查看答案和解析>>
科目: 来源: 题型:解答题
 已知二次函数y=x2-4x+3,设该抛物线与y轴交于点C,抛物线顶点为D,点P是x轴上的点,且满足PC+PD最短.
已知二次函数y=x2-4x+3,设该抛物线与y轴交于点C,抛物线顶点为D,点P是x轴上的点,且满足PC+PD最短.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,二次函数y=ax2+bx+c的图象与x轴交于点A(6,0)和点B(2,0),与y轴交于点C(0,2$\sqrt{3}$),⊙P经过点A、B、C三点.
如图,二次函数y=ax2+bx+c的图象与x轴交于点A(6,0)和点B(2,0),与y轴交于点C(0,2$\sqrt{3}$),⊙P经过点A、B、C三点.查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OA、OC的长(OA<OC)是方程x2-4x+3=0的两个根,且抛物线的对称轴是直线x=1.
如图,抛物线y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OA、OC的长(OA<OC)是方程x2-4x+3=0的两个根,且抛物线的对称轴是直线x=1.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com