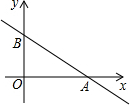1．如图：直线y=kx+3与x轴、y轴分别交于A、B两点，tan∠OAB=$\frac{3}{4}$，点C（x，y）是直线y=kx+3上与A、B不重合的动点．
（1）求直线y=kx+3的解析式；
（2）当点C运动到什么位置时△AOC的面积是4．

20．如图是一枚六面体骰子的展开图，则掷一枚这样的骰子，朝上一面的数字是朝下一面的数字的3倍的概率是（　　）

A．

$\frac{1}{2}$

B．

$\frac{1}{3}$

C．

$\frac{1}{4}$

D．

$\frac{1}{6}$

19．已知AB是⊙O的直径，弦CD⊥AB于O，F是DC延长线上的一点，FA、FB与⊙O分别交于M、G，GO延长线与⊙O交于N．
（1）求证：AB平分∠MAN；
（2）如图（2），若弦CD⊥OB于E，请判断AB是否仍平分∠MAN，并说明理由；
（3）在（2）的条件下，若⊙O的半径为5，FE=2CE=6，求线段AN的长．

18．在Rt△ABC中，∠C=90°，AC=2，BC=1，则sinA=$\frac{\sqrt{5}}{5}$．

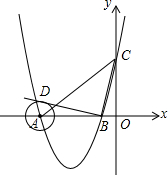17．如图，在平面直角坐标系中，顶点为（-3，-4）的抛物线交x轴于A、B两点（点A在点B的左侧），交y轴于C点，已知C点坐标为（0，5）．
（1）求此抛物线的解析式；
（2）过点B作线段BC的垂线交抛物线于点D，若以点A为圆心的圆与直线BD相切，求⊙A半径；
（3）在抛物线上是否存在一点P，使△ACP是以AC为直角边的三角形？若存在，求出点P的坐标；若不存在，请说明理由．

16．已知二次函数y=x²-4x．
（1）在给出的直角坐标系内用描点法画出该二次函数的图象；
（2）根据所画的函数图象写出当x在什么范围内时，y≤0？
（3）根据所画的函数图象写出方程：x²-4x=5的解．

15．如图，在直角梯形ABCD中，AD∥BC，∠C=90°，AD=3，以A为中心将腰AB顺时针旋转90°至AE，连接DE，若AB=5，CD=3，则BC的长为（　　）

A．

5

B．

6

C．

7

D．

8

14．“十字相乘法”能把二次三项式分解因式，对于形如ax²+bxy+cy²的x，y二次三项式来说，方法的关键是把x²项系数a分解成两个因数a₁，a₂的积，即a=a₁•a₂，把y²项系数c分解成两个因数，c₁，c₂的积，即c=c₁•c₂，并使a₁•c₂+a₂•c₁正好等于xy项的系数b，那么可以直接写成结果：ax²+bxy+cy²=（a₁x+c₁y）（a₂x+c₂y）
例：分解因式：x²-2xy-8y²
解：如右图，其中1=1×1，-8=（-4）×2，而-2=1×（-4）+1×2∴x²-2xy-8y²=（x-4y）（x+2y）
而对于形如ax²+bxy+cy²+dx+ey+f的x，y的二元二次式也可以用十字相乘法来分解，
如图1，将a分解成mn乘积作为一列，c分解成pq乘积作为第二列，f分解成jk乘积作为第三列，如果mq+np=b，pk+qj=e，mk+nj=d，即第1，2列、第2，3列和第1，3列都满足十字相乘规则，则原式=（mx+py+j）（nx+qy+k）；

例：分解因式：x²+2xy-3y²+3x+y+2
解：如图2，其中1=1×1，-3=（-1）×3，2=1×2；
而2=1×3+1×（-1），1=（-1）×2+3×1，3=1×2+1×1；∴x²+2xy-3y²+3x+y+2=（x-y+1）（x+3y+2）
请同学们通过阅读上述材料，完成下列问题：
（1）分解因式：6x²-7xy+2y²=（2x-y）（3x-2y）x²-6xy+8y²-5x+14y+6=（x-2y-2）（x-4y-3）
（2）若关于x，y的二元二次式x²+7xy-18y²-5x+my-24可以分解成两个一次因式的积，求m的值．
（3）已知x，y为整数，且满足x²+3xy+2y²+2x+4y=-1，求x，y．

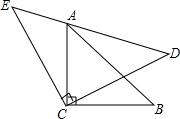13．如图，在等腰直角三角形Rt△ABC和Rt△ECD中，Rt△ACB的顶点A在Rt△ECD的斜边ED上，求证：AE²+AD²=2AC²．（提示：添加辅助线连接BD）

12．如图，已知△ABC是边长为1的等腰直角三角形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，则第五个等腰直角三角形的斜边AG长为（　　）

A．

4$\sqrt{2}$

B．

5$\sqrt{2}$

C．

4$\sqrt{3}$

D．

5$\sqrt{3}$