
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
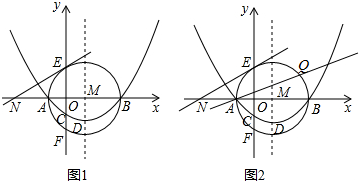
 如图,抛物线y=ax2+bx+c(a≠0)交x轴于点A,点B,交y轴于点E,其中B点的坐标为(3,0),OB=3OA,连接AE,tan∠EAO=3,直线y=-2x-2交x轴于点C,交y轴于点D.
如图,抛物线y=ax2+bx+c(a≠0)交x轴于点A,点B,交y轴于点E,其中B点的坐标为(3,0),OB=3OA,连接AE,tan∠EAO=3,直线y=-2x-2交x轴于点C,交y轴于点D.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
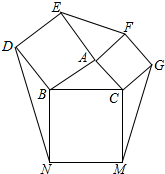 如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN
如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
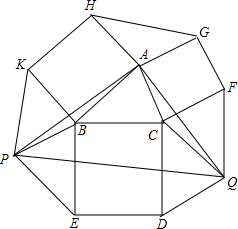 如图,已知△ABC,分别以AB、AC、BC作边作正方形ABKH、正方形ACFG、正方形BCDE,作?BEPK,?CDQF,联结AP,AQ,PQ,求证:△APQ是等腰直角三角形.
如图,已知△ABC,分别以AB、AC、BC作边作正方形ABKH、正方形ACFG、正方形BCDE,作?BEPK,?CDQF,联结AP,AQ,PQ,求证:△APQ是等腰直角三角形.查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
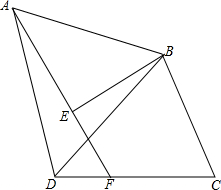 已知等边△ABD中,点E为△ABD内部一点,连接AE、BE,使得∠AEB=90°,过B作BC⊥BE,连接CD,使∠DCB=60°,延长AE交CD于点F,若AE:DC=5:7,且DE•EF=8,则四边形AFCB的面积.
已知等边△ABD中,点E为△ABD内部一点,连接AE、BE,使得∠AEB=90°,过B作BC⊥BE,连接CD,使∠DCB=60°,延长AE交CD于点F,若AE:DC=5:7,且DE•EF=8,则四边形AFCB的面积.查看答案和解析>>
科目: 来源: 题型:解答题
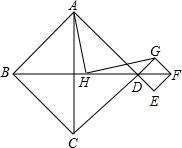 四边形ABCD与四边形DEFG都是正方形,点H为BF的中点,连接HA,HG.若三点B、D、F在同一直线上,如图探索HA与HG的数量及位置关系,并予以证明.
四边形ABCD与四边形DEFG都是正方形,点H为BF的中点,连接HA,HG.若三点B、D、F在同一直线上,如图探索HA与HG的数量及位置关系,并予以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com