
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
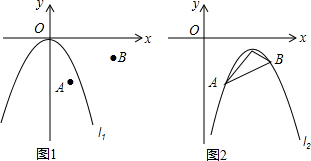
 2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;
2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
 如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )
如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目: 来源: 题型:解答题
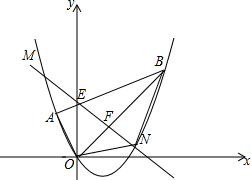 如图,平面直角坐标系xOy中点A的坐标为(-1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
如图,平面直角坐标系xOy中点A的坐标为(-1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.查看答案和解析>>
科目: 来源: 题型:选择题
 如图,Rt△ABC中,∠B=90°,BC=12,tanC=$\frac{3}{4}$.如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且$\frac{{A{P_0}}}{AB}=\frac{{A{P_1}}}{AC}$;第二步从P1跳到BC边的P2(第2次落点)处,且$\frac{{C{P_1}}}{AC}=\frac{{C{P_2}}}{BC}$;第三步从P2跳到AB边的P3(第3次落点)处,且$\frac{{B{P_2}}}{BC}=\frac{{B{P_3}}}{AB}$;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为( )
如图,Rt△ABC中,∠B=90°,BC=12,tanC=$\frac{3}{4}$.如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且$\frac{{A{P_0}}}{AB}=\frac{{A{P_1}}}{AC}$;第二步从P1跳到BC边的P2(第2次落点)处,且$\frac{{C{P_1}}}{AC}=\frac{{C{P_2}}}{BC}$;第三步从P2跳到AB边的P3(第3次落点)处,且$\frac{{B{P_2}}}{BC}=\frac{{B{P_3}}}{AB}$;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
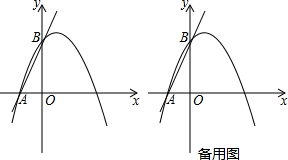
 如图,在平面直角坐标系中,直线AB和抛物线交于点A(-4,0),B(0,4),且点B是抛物线的顶点.
如图,在平面直角坐标系中,直线AB和抛物线交于点A(-4,0),B(0,4),且点B是抛物线的顶点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com