13．如图是由若干个粗细均匀的铁环最大限度地拉伸组成的链条．已知铁环粗0.8厘米，每个铁环长5厘米．设铁环间处于最大限度的拉伸状态．若要组成1.75米长的链条，则需要51个铁环．

12．探究发现：阅读解答题：在数学中，有些大数值问题可以通过用字母代替数转化成整式问题来解决．例：试比较20142015×20142012与20142014×20142013的大小．
解：设20142014=a，x=20142015×20142012，
用这种方法不仅可比大小，也能解计算题哟！
y=20142014×20142013
那么x=（a+1）（a-2），
那么y=a（a-1）
∵x-y=-2＜0
∴x＜y（填＞、＜或=）．
填完后，你学到了这种方法吗？不妨尝试一下，相信你准行！
（1）将上述解答补充完整
x-y=-2＜0；x＜y（填＞、＜或=）
（2）计算3.456×2.456×5.456-3.456³-1.456²．
（3）计算：
（1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$-$\frac{1}{5}$）（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$）-（1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$-$\frac{1}{5}$-$\frac{1}{6}$）（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$）

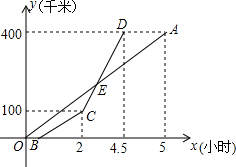11．甲乙两地相距400千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段OA表示货车离甲地的路程y（千米）与所用时间x（小时）之间的函数关系，折线BCD表示轿车离甲地的路程y（千米）与x（小时）之间的函数关系，根据图象解答下列问题：
（1）求线段CD对应的函数表达式；
（2）求E点的坐标，并解释E点的实际意义；
（3）若已知轿车比货车晚出发20分钟，且到达乙地后在原地等待货车，在两车相遇后当货车和轿车相距30千米时，求货车所用时间．

10．计算$\overrightarrow{a}$-$\frac{1}{2}$（$\overrightarrow{a}$-4$\overrightarrow{b}$）=$\frac{1}{2}\overrightarrow{a}$+2$\overrightarrow{b}$．

9．去年我省规划重建校舍约3876000平方米，这个数精确到十万位并用科学记数法表示为（　　）

A．

3.8×106平方米

B．

3.8×107平方米

C．

3.9×106平方米

D．

3.9×107平方米

8．如图，由正三角形OAB绕点O经过连续5次旋转后得到正六边形ABCDEF，那么每次旋转的旋转角的大小是（　　）

A．

30°

B．

60°

C．

90°

D．

150°

7．在△ABC中，点E，F分别为AB，AC的中点，连接CE，BF，CE与BF交于点M，且CE⊥BF，连接EF．
（1）如图1，当∠FEC=45°，EF=2$\sqrt{2}$时，①填空：BC=4$\sqrt{2}$；BF=6．
②求证：AB=AC；
（2）如图2，当∠FEC=30°，BC=8时，求CE和AB的长度；
（3）如图3，在?ABCD中，E，F分别是BC，AD的中点，连接AC，BF，AC与BF交于点M，且BF⊥AC，连接AE，EF，AE与BF交于点G，EF与AC交于点H，求$\frac{GM}{MF}$的值．

6．发现：
（1）若干平面上三点能够确定一个圆，那么这三点所满足的条件是三点不在同一条直线上．
（2）我们判断四个点A，B，C，D（任意其中个三点不共线）是否在同一圆上时，一般地，先作过A，B，C三点的圆，然后判断点D是否在这个圆上，如果在，则这四个点共圆，如果不在，则不存在同时过这四个点的圆．
思考：
（1）如图1，∠ACB=∠ADB=90°，那么点A，B，C，D四点在（填“在”或“不在”）同一个圆上；
（2）如图2，如果∠ACB=∠ADB=a（a≠90°），（点C，D在AB的同侧），那么点D还在经过A，B，C三点的圆上吗？芳芳已经证明了点D不在圆内（如图所示），只要能够证明点D也不再圆外，就可以判断点D一定在圆上了，请你完成证明过程．
芳芳的证明过程：
如图3，过A，B，C三点作圆，圆心为O．假设点D在⊙O内，设AD的延长线交⊙O于点P，连接BP．易得∠APB=∠ACB．又由∠ADB是△BPD的外交，得到∠ADB＞∠APB，因此∠ADB＞∠ACB，这个结论与条件中的∠ACB=∠ADB矛盾，所以点D不在圆内．
应用：
如图4，在四边形ABCD中，连接AC，BD，∠CAD=∠CBD=90°，点P在CA的延长线上，连接DP．若∠ADP=∠ABD．求证：DP为Rt△ACD的外接圆的切线．

5．在直角梯形ABCD中，AD∥BC，∠DAB=90°，AD=1，BC=2．连接BD，把△ABD绕着点B逆时针旋转90°得到△EBF，若点F刚好落在DA的延长线上，则∠C=45°．

4．根据要求，用四舍五入法取下列各数的近似数．
（1）146491≈1.5×10⁵（精确到万位）；  
（2）3952≈4.0×10³（精确到百位）