
科目: 来源: 题型:解答题
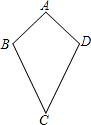 【问题提出】
【问题提出】查看答案和解析>>
科目: 来源: 题型:填空题
 如图,正方形ABCD的边长为1,P为BC上任意一点(含B、C两点),分别过点B、C、D作射线AP的垂线,垂足分别为E、F、G,以下判断:
如图,正方形ABCD的边长为1,P为BC上任意一点(含B、C两点),分别过点B、C、D作射线AP的垂线,垂足分别为E、F、G,以下判断:查看答案和解析>>
科目: 来源: 题型:选择题
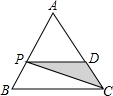 如图,P为等边三角形ABC中AB边上的动点,沿A→B的方向运动,到达点B时停止,过P作PD∥BC.设AP=x,△PDC的面积为y,则y关于x的函数图象大致为( )
如图,P为等边三角形ABC中AB边上的动点,沿A→B的方向运动,到达点B时停止,过P作PD∥BC.设AP=x,△PDC的面积为y,则y关于x的函数图象大致为( )| A. | 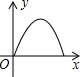 | B. | 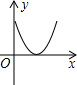 | C. | 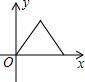 | D. | 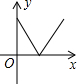 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
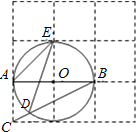 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的余弦值等于( )
如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的余弦值等于( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com