
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
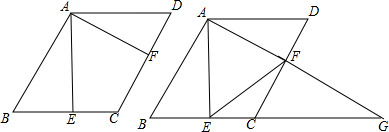
查看答案和解析>>
科目: 来源: 题型:解答题
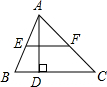 如图,已知在△ABC中,AD⊥BC,垂足为点D,若AD=$\frac{1}{2}$BC,EF为中位线,那么以EF为直径的圆与直线BC有怎样的位置关系?请说明理由.
如图,已知在△ABC中,AD⊥BC,垂足为点D,若AD=$\frac{1}{2}$BC,EF为中位线,那么以EF为直径的圆与直线BC有怎样的位置关系?请说明理由.查看答案和解析>>
科目: 来源: 题型:解答题
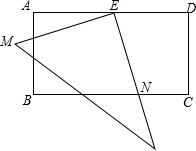 在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.
在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.查看答案和解析>>
科目: 来源: 题型:填空题
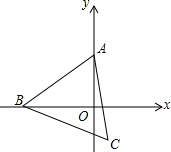 如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是($\sqrt{3}$,1).随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是y=$\sqrt{3}$x-2.
如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是($\sqrt{3}$,1).随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是y=$\sqrt{3}$x-2.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
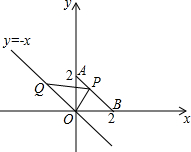 如图,在平面直角坐标系中,点A的坐标是(0,2),点B的坐标是(2,0),连结AB,点P是线段AB上的一个动点(包括两端点),直线y=-x上有一动点Q,连结OP,PQ,已知△OPQ的面积为$\sqrt{2}$,则点Q的坐标为($\sqrt{2}$,-$\sqrt{2}$)或(-$\sqrt{2}$,$\sqrt{2}$)..
如图,在平面直角坐标系中,点A的坐标是(0,2),点B的坐标是(2,0),连结AB,点P是线段AB上的一个动点(包括两端点),直线y=-x上有一动点Q,连结OP,PQ,已知△OPQ的面积为$\sqrt{2}$,则点Q的坐标为($\sqrt{2}$,-$\sqrt{2}$)或(-$\sqrt{2}$,$\sqrt{2}$)..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com